ในโพสต์นี้เราจะมาพูดถึงฟิสิกส์กันบ้างหลังจากโพสต์ก่อนหน้าเราพูดถึงโปรแกรมมิ่งไปซะเยอะ ทุกคนที่เรียนวิชาฟิสิกส์ต้องเคยผ่านการเรียนกฎของนิวตันกันมา ไม่ว่าจะรุ่นไหน เราก็เรียนกฎของนิวตัน \( F = ma \) ท่องจำกันอย่างขึ้นใจตั้งแต่สมัย ม.2 หรือ ม.3 แถมแก้สมการการเคลื่อนที่จากกฎของนิวตันได้อย่างไม่ยากเย็น เราก็เช่นกัน
แต่เราพอโตขึ้นมา ได้เรียนหลายวิชามากขึ้น เราก็คนพบว่า เห้ย! จริงๆ แล้วไม่ใช่แค่กฎของนิวตันที่ใช้แก้สมการการเคลื่อนที่ได้นะ ยังมีสมการที่เรียกว่าสมการออยเลอร์-ลากรานจ์ (Euler-Lagrange equation) หรือเรียกสั้นๆว่าสมการลากรานจ์ ที่แก้สมการการเคลื่อนที่ของวัตถุได้เช่นกัน คือจริงๆสำหรับนักเรียนทั่วไปอาจจะไม่เจอสมการนี้กันมากเท่าไหร่ แต่สำหรับคนที่อ่านเปเปอร์ในสายวิศวกรรมควบคุมหรือ Control ทีไร มักจะเจอการพูดถึงสมการนี้โดยประจำ แถมไม่ค่อยจะแก้สมการมาให้อีกด้วย ชอบทิ้งสมการไว้ใช้แก้สมการการเคลื่อนที่เอง หรือ State equation
กลับมาที่สมการลากรานจ์ มันค่อนข้างจะมหัศจรรย์เล็กน้อย แต่ว่าหลักการของสมการนี้คือเราสามารถเขียนสมการการเคลื่อนที่ได้จากเพียงพลังงานศักย์ พลังงานจลน์ และความรู้แคลคูลัส (ดิฟ ดิฟ ดิฟ) เท่านั้น แน่นอนว่าเราจะไม่ลงรายละเอียดการพิสูจน์สมการเนื่องจากต้องใช้ความรู้ Calculus of Variation ถึงจะพิสูจน์สมการลากรานจ์ได้ อันนั้นไว้สำหรับให้คนที่เรียน Optimal Control อย่างนักศึกษาภาคไฟฟ้าหรือเครื่องกลเท่านั้น
ข้อดีขอการใช้สมการลากราจน์นี้คือเราสามารถเช็คสมการการเคลื่อนที่ได้จากเพียงพลังงานจลน์และพลังงานศักย์อย่างไม่ยากนัก และเราไม่ต้องแตกแรงและแก้หลายๆสมการอย่างการใช้กฎของนิวตันอีกด้วย ยกตัวอย่างสมการการเคลื่อนที่ ที่เขียนด้วยสมการลากรานจ์ได้ง่ายๆเลยก็เช่น single pendulum, double pendulum หรือแม้แต่ triple pendulum ก็ยังได้อยู่ หรือการเขียน inverted pendulum ก็ไม่ยากเพราะว่าเราเขียนสมการของพลังงานสำหรับ inverted pendulum ง่ายกว่าใช้กฎของนิวตันแน่ๆ
โดยถ้าเราเขียนสมการของพลังงานถูกต้อง (ซึ่งง่ายกว่าการเขียนสมการนิวตันเยอะมาก) ก็จะมีโอกาสเขียนสมการการเคลื่อนที่ได้ถูกต้องมากกว่าการใช้กฎของนิวตัน และเราสามารถเอาลากรานจ์ที่เขียนไปแก้แบบ Symbolic โดยใช้ solver ในโปรแกรมต่างๆ Mathematica, sympy บน Python หรือ Matlab ก็ได้ สำหรับ Mathematica การหาสมการการเคลื่อนที่โดยใช้โค้ดเขียนแค่ 3-4 บรรทัดเท่านั้น คือจริงๆไม่สั้นขนาดนั้นนะ แต่ว่าไม่ยาวมาก ในตัวอย่างด้านล่าง เราจะใช้ Mathematica เป็นตัวอย่างในการแก้สมการ
ไม่ใช่แค่เพียงเท่านี้ ยังมีอีกหลายอย่างที่สมการลากรานจ์สามารถทำได้ เช่น การใส่โมเมนตัม การใส่ constraint เข้าไปในวิถีที่วัตถเคลื่อนที่เช่นวัตถุวิ่งอยู่บนราง หรือแม้แต่ใส่แรงเข้าไปในสมการก็ได้เช่นกัน ซึ่งเราจะไม่พูดถึงในโพสต์นี้
โอเค จะให้อธิบายสมการออยเลอร์-ลากรานจ์ ไปมากกว่านี้ก็ยังได้ แต่เนื้อหาโดยละเอียดน่าจะมีตามหนังสือวิชาการหรือแม้แต่บน Wikipedia เราจะมาลองเขียนสมการกันจริงๆเลยในโพสต์นี้ เราจะใช้ single pendulum และ double pendulum เป็นตัวอย่าง พร้อมตัวอย่างโค้ด snippet ให้ไปลองเขียนกันบน Mathematica กัน
Euler-Lagrange equation basic and terminology
ก่อนจะเริ่มต้นกันด้วยการเขียนสมการลากรานจ์ เราต้องรู้จักการเขียนตัวแปรที่เรียกกันว่าลากรานเจียน (Lagrangian) หรือใช้สัญลักษณ์ว่า \(L\) กันก่อน ซึ่งคือพลังงานจลน์ของระบบลบกับพลังงานศักย์
\[L = KE - PE\]เมื่อ \(KE\) คือพลังงานจลน์ ส่วน \(PE\) คือพลังงานศักย์
ส่วนสมการออยเลอร์-ลากรานจ์ (Euler-Lagrange Equation) เขียนได้ดังนี้
\[\cfrac{d}{dt}\cfrac{\partial L}{\partial \dot{q}} = \cfrac{\partial L}{\partial q}\]เมื่อ \(q\) คือเวกเตอร์ของตัวแปรในระบบ สมมติเราแค่เขียนสมการของ single pendulum ตัวแปรก็คือแค่ \(\theta\) นั่นเอง ถ้า double pendulum ก็จะเป็น \( \theta_1, \theta_2 \) เป็นต้น
เมื่อเราเขียนและแก้สมการลากรานจ์ทั้งหมดแล้ว ก็จะได้มาการการเคลื่อนที่ของวัตถุมานั่นเอง เช่น สมมติว่า \(q = [x, y]^T\) ก็จะมีสมการลากรานจ์ 2 สมการ ซึ่งแก้ได้ทั้งหมด 2 differential equation
ตัวอย่างที่ 1: ก้อนมวลตกลงบนพื้น
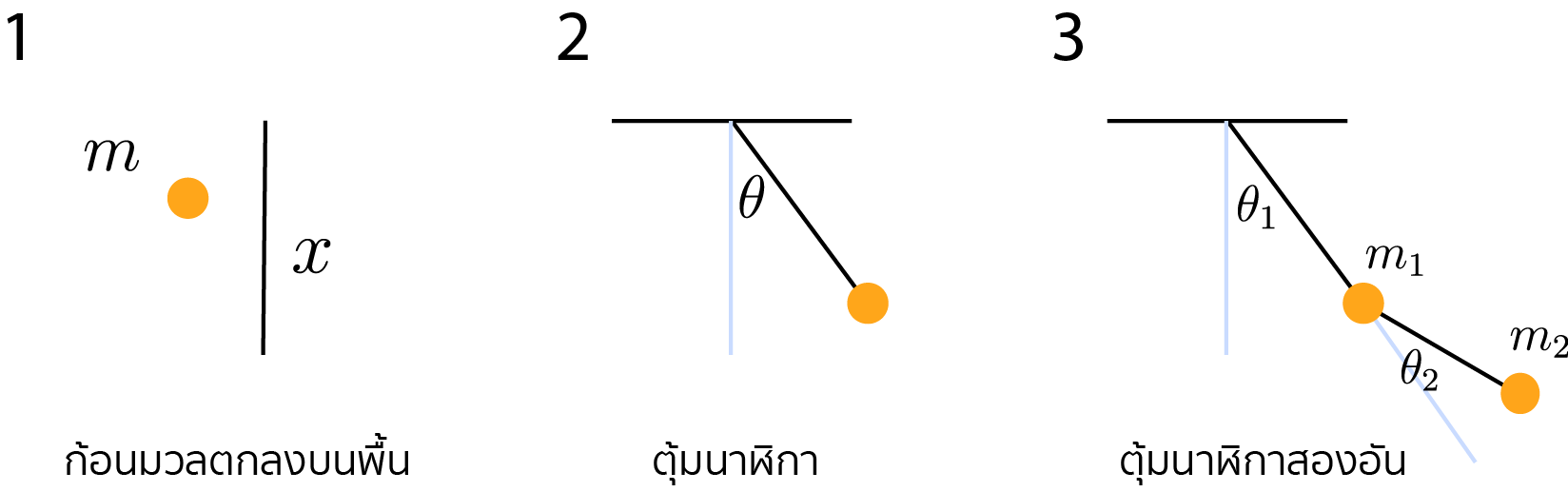
จุดมวล \(m\) ตกลงบนพื้นด้วยแรงโน้มถ่วง \(g\) โดยเรากำหนดให้ \(x\) เป็นความสูงของวัตถุเทียบกับพื้น ในที่นี้ตัวแปร \(q\) คือ \(x\) นั่นเอง เขียนพลังงานจลน์ได้ว่า \(KE = \frac{1}{2}m\dot{x}^2 \) ส่วนพลังงานศักย์ \(PE = mgx \) ในที่ ดังนั้นเราเขียน Lagrange ได้ดังต่อไปนี้
\[L = KE - PE = \frac{1}{2}m\dot{x}^2 - mgx\]ด้านซ้ายของสมการลากรานจ์เขียนได้ดังนี้ \( \cfrac{d}{dt}\cfrac{\partial L}{\partial \dot{x}} = \cfrac{d}{dt}m\dot{x} = m\ddot{x} \)
ส่วนด้านขวาของสมการคือ \( \cfrac{\partial L}{\partial x} = -mg \)
ดังนั้นเมื่อใส่เข้าไปในสมการลากรานจ์ จะได้ \( m\ddot{x} = -mg, \ddot{x} = -g \) เป็นสมการการเคลื่อนที่ของก้อนมวลนี้ ซึ่งได้เหมือนกฎของนิวตันเป๊ะเลย เจ๋งมาก!
ตัวอย่างที่ 2: ตุ้มนาฬิกาหรือ single pendulum
สำหรับ single pendulum \(q\) ในที่นี้คือ \(\theta\) นั่นเอง โดยเราเขียนพลังงานจลน์ได้ว่า \( KE = \frac{1}{2} mv^2 = \frac{1}{2}m(L \dot{\theta})^2 \) ส่วนพลังงานศักย์เมื่อให้จุดต่ำสุดที่ pendulum ไปถึงเป็นจุดเทียบ เขียนได้ว่า \( PE = mgh = mgL(1 - \cos(\theta))\) ดังนั้นเราเขียนลากรานจ์ได้ดังต่อไปนี้
\[L = KE - PE = \frac{1}{2}m(L \dot{\theta})^2 - mgL(1 - \cos(\theta))\]ด้านซ้ายของสมการลากรานจ์ \( \cfrac{d}{dt}\cfrac{\partial L}{\partial \dot{\theta}} = \cfrac{d}{dt}(mL^2\dot{\theta}) = mL^2 \ddot{\theta} \)
ด้านขวาของสมการลากรานจ์เป็นประมาณนี้ (โน้ตไว้ว่า \( \cfrac{d}{d\theta}\cos(\theta) = -\sin(\theta) \) อันนี้คนเรียนแคลคูลัสน่าจะจำได้ ขนาดเมาก็ยังต้องดิฟได้ ถือเป็นการเช็ค) \( \cfrac{\partial L}{\partial \theta} = -mgL\sin(\theta) \)
ดังนั้นสมการการเคลื่อนที่จึงเขียนได้ดังนี้ \( mL^2 \ddot{\theta} = -mgL\sin(\theta) \) หรือว่า \( \ddot{\theta} = -\cfrac{g}{L}sin(\theta) \)
ตัวอย่างที่ 3: ตุ้มนาฬิกาสองอัน หรือ double pendulum
วิธีการก็เหมือนกันกับ single pendulum เป๊ะ แค่เราต้องเขียนพลังงานจลน์และพลังงานศักย์ของมวลอีกก้อนเพิ่ม diagram ของ double pendulum ดูได้จากข้างบน สำหรับสมการนั้นเราจะไปแก้กันโดยใช้ Mathematica เลย เราจะไม่เขียนลงไปในโพสต์ แต่เชื่อว่าผู้ที่อ่านมาถึงจุดนี้สามารถลองเช็คคำตอบของตัวเองได้กับ Mathematica โดยตรงเลย
ในที่นี้ \(q = [\theta_1, \theta_2] \) นั่นเองดังนั้นหลังจากเขียน \(L\) เราจะได้สมการลากรานจ์ทั้งหมดสองสมการ
\[\cfrac{d}{dt}\cfrac{\partial L}{\partial \dot{\theta_1}} = \cfrac{\partial L}{\partial \theta_1}\]และ
\[\cfrac{d}{dt}\cfrac{\partial L}{\partial \dot{\theta_2}} = \cfrac{\partial L}{\partial \theta_2}\]จากสองสมการนี้เราสามารถแก้หา \( \ddot{\theta}_1, \ddot{\theta}_2 \) ได้โดยใช้คำสั่ง Solve ของ Mathematica
ก่อนจะไปดูโค้ดเพื่อแก้สมการ เราลองมาเขียนกันลากรานจ์ดูก่อน จะได้อ่านโค้ดเข้าใจมากขึ้น
\[KE = KE_{m_1} + KE_{m_2} = \frac{1}{2}m_1 (\dot{x}_1^2 + \dot{y}_1^2) + \frac{1}{2}m_2 (\dot{x}_2^2 + \dot{y}_2^2)\]โดยที่
\[x_1 = R_1\sin\theta_1, y_1 = -R_1\cos\theta_1\]และ
\[x_2 = R_1\sin\theta_1 + R_2\sin(\theta_1 + \theta_2), y_2 = -R_1\cos\theta_1 - R_2\cos(\theta_1 + \theta_2)\]ส่วนพลังงานศักย์ เขียนได้ดังนี้
\[PE = -m_1 g R_1 \cos\theta_1 + m_2 g (-R_1 \cos\theta_1 - R_2 \cos(\theta_1 + \theta_2))\]จากนั้นเมื่อเราแทนทุกอย่างลงไปในสมการจะได้ลากรานจ์ \(L\) ตามในโค้ดที่ให้ด้านล่าง
จริงๆส่วนของการแก้สมการจบแค่ช่วงแรกเท่านั้น แต่เนื่องจากเราต้องการเอาค่าของ \( \theta_1, \theta_2 \) จากเวลา 0 ถึง 50 มาพล้อตเป็นแบบแอนิเมชั่นด้วย จึงต้องใช้ NDSolve ของ Mathematica เพื่อแก้สมการ

สรุป
มาถึงจุดนี้คนเขียนโพสต์ก็ได้สลบลงหน้าคอมพิวเตอร์ (พูดเล่นนะ)
ถ้าใครลองเอาโค้ดไปรันบน Mathematica ก็ลองเปลี่ยนพารามิเตอร์ได้ตามชอบเลยตั้งแต่ขนาดของมวล รวมถึง gravitational constant เป็นต้น เพื่อดูว่าส่งผลต่อ double pendulum อย่างไรบ้าง ใครที่สนใจลองเขียนสมการอื่นๆ เราแนะนำให้ลองเขียนลากรานจ์ของระบบที่เราสนใจ อาจจะเป็น inverted pendulum ก็ได้ (\(x(t), \theta(t) \)) แล้วก็ลองใส่และแก้สมการใน Mathematica ดูว่าสมการที่เราเขียนนั้นถูกหรือไม่
สำหรับคนที่ชอบฟิสิกส์ก็สามารถเอาเทคนิคนี้ไปเขียนสมการการเคลื่อนที่ในระบบที่แปลกๆได้อย่างไม่ยากนัก ส่วนคนที่ชอบ simulation ก็สามารถลองเขียน simulation ฟิสิกส์ง่ายๆได้ผ่าน Mathematica และสำหรับคนที่เรียน Control โดยตรงอย่างเช่นนักศึกษาภาคไฟฟ้าหรือภาคเครื่องกล คราวนี้ก็ไม่ต้องกลัวเวลาเจอเปเปอร์ Optimal Control แล้วมีสมการหน้าตาประมาณ \( \cfrac{d}{dt}\cfrac{\partial L}{\partial \dot{q}} = \cfrac{\partial L}{\partial q} \) นี้แล้ว :)
