สวัสดีอีกครั้งกับ tupleblog ไม่ได้เขียนบล็อกซะนานเลย เห็นบล็อกที่แล้วเขียนไปเมื่อปีที่แล้วค่อนข้างตกใจนิดหน่อย
วันนี้เราจะมาทำความรู้จักกับการเรียนรู้แบบเสริมกำลังหรือ reinforcement learning กัน พอเข้าใจว่ามีคนเขียนหัวข้อนี้กันไปเยอะพอสมควรแล้ว แต่ในบล็อกนี้เราจะมาเริ่มต้นกันตั้งแต่พื้นฐานดังต่อไปนี้
- Reinforcement Learning (RL) คืออะไร
- ทำความเข้าใจโจทย์ Reinforcement learning และ Finite Markov Decision Process (MDP)
- หา Optimal Policy โดยใช้วิธี Monte Carlo และ Temporal Difference (ใช้ grid world เป็นตัวอย่าง)
- แปลง Discrete Reinforcement Learning เป็น Continuous Reinforcement Learning ได้ยังไงนะ
- Continuous Reinforcement Learning โดยใช้ Deep Neural Network
- ตัวอย่างไลบรารี่ที่สร้าง environment สำหรับ reinforcement learning
- และปิดท้ายด้วยเทคนิคต่างๆที่เราไม่ได้กล่าวถึงในโพสต์นี้นะฮะ
ส่วนใครที่อยากจะอ่านแบบเต็มๆ จริงๆจังๆหลังจากอ่านโพสต์นี้ ลองไปอ่านกันได้ในหนังสือ “Reinforcement Learning, An Introduction” ซึ่งเขียนโดย Richard Sutton and Andrew Barto นะฮะ ต้องยอมรับว่าหนังสือนี่ยาวกว่า
Reinforcement learning คืออะไร
Reinforcement Learning เป็นวิธีการเรียนรู้แบบนึงที่โดยการเรียนรู้เกิดมาจากการปฎิสัมพันธ์ (interaction) ระหว่างผู้เรียนรู้ (agent) กับสื่งแวดล้อม (environment) ตัวอย่างของ Reinforcement Learning ได้แก่
- ถ้าเราเกิดเป็นน้องหมาและเราหิวพอดี เราอยากจะได้อาหาร สิ่งแรกที่เราทำนั่นก็คือหันไปดูว่ามีใครอยู่ใกล้ๆบ้างนะ โอ้! เจ้าของอยู่ใกล้ๆพอดีเลย เรายืนมือออกไป ร้องขออาหารกับเจ้าของ และหลังจากเราขอแล้วสิ่งที่เราได้กลับมาคืออาหารนั่นเอง
- การเล่น Blackjack สมมติเราเป็นผู้เล่นและอยากจะได้เงินมากที่สุดจากการเล่น สิ่งที่เราควรทำก็คือต้องพนันอย่างเหมาะสม ถ้าช่วงไหนที่ไพ่คะแนนต่ำๆออกไปเยอะ เราก็ควรจะแทงสูงขึ้นเป็นต้น (หรือเรียกว่าเทคนิคไฮ-โลนั่นเอง)
- การเล่น Counter Strike ถ้าเราเป็นผู้เล่น ก็ต้องสังเกตว่ามีศตรูอยู่ใกล้ๆหรือไม่ ถ้ามีศตรูเราต้องหันไปทางศตรูและกดยิงเพื่อจะให้เราได้แต้มเยอะกว่าศตรู
- เวลาเราแชทกับสาว เราควรจะแชทยังไงให้บทสนทนายาวนานและทำให้สาวแชทกับเราได้นานที่สุด
ในตัวอย่างของน้องหมา การที่น้องหมาสำรวจสิ่งรอบตัวแล้วลองทำอะไรซักอย่างและได้ผลลัพธ์กลับมานั้นเราสามารถเขียนเป็นสมการคณิตศาสตร์ได้ โดยความเจ๋งของ reinforcement learning ก็คือว่าถ้าเราลองสำรวจและทำอะไรซักอย่างกับโลกไปเรื่อยๆ จะทำให้เราเรียนรู้มากขึ้นเรื่อยๆได้ เช่นในกรณีที่เจ้าของน้องหมาบอกให้นั่งนิ่งๆ ถ้านั่งแล้วจะได้กินขนม แต่ถ้าน้องหมาเดินไปเดินมาก็จะอดกินนั่นเอง แต่ถ้าฝึกไปบ่อยๆ น้องหมาก็จะเข้าใจว่า อ๋อ ถ้าได้รับคำสั่งนี้จะต้องทำแบบนี้นี่เอง
ทำความเข้าใจโจทย์ Reinforcement learning
ก่อนที่เราจะมาแก้ปัญหาว่าเราจะเรียนรู้ได้ยังไงโดยใช้ Reinforcement Learning เราจะมาเขียนแผนผังกันดูว่าหน้าตาของโจทย์ที่เราจะแก้ มีหน้าตาจะเป็นยังไงนะ
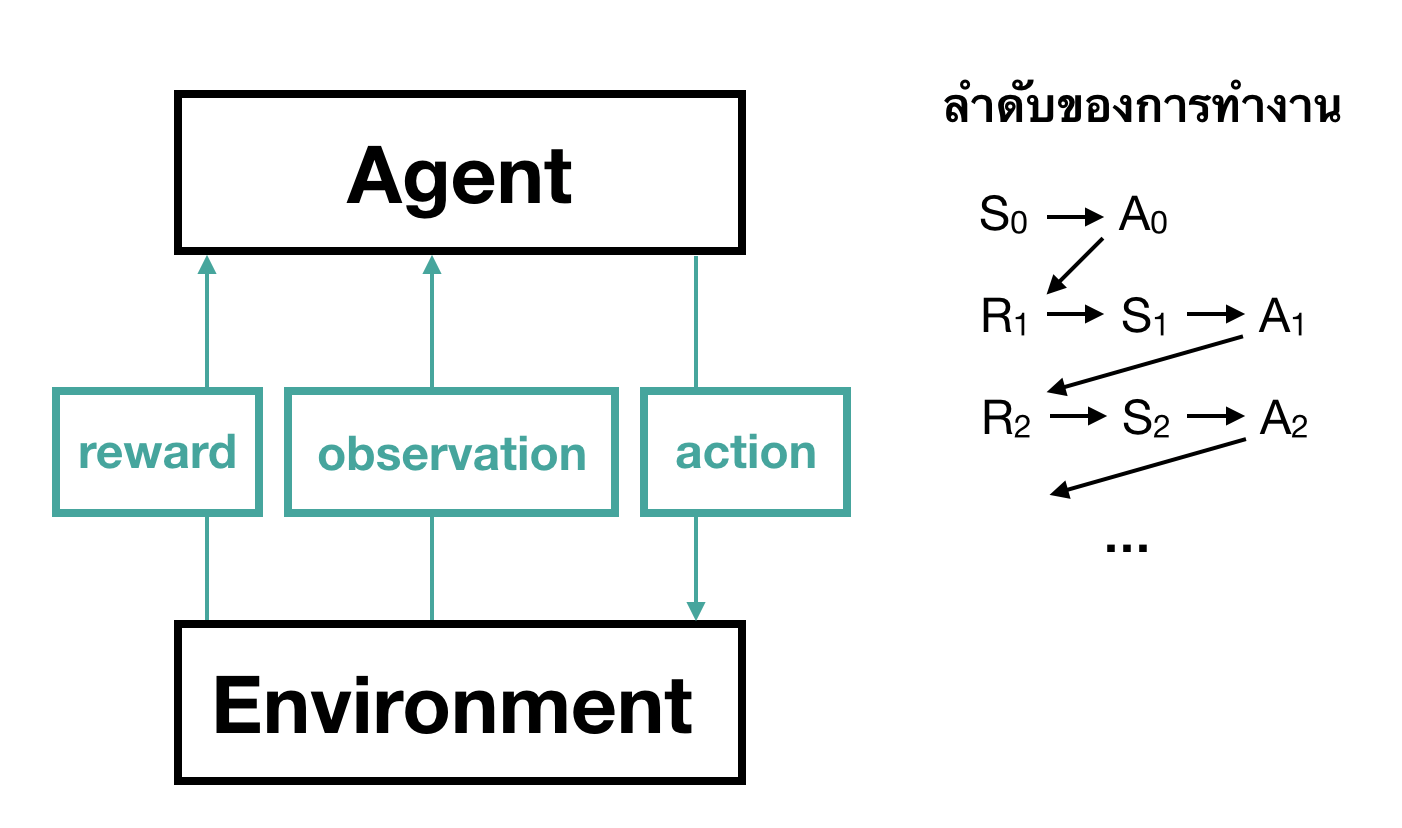
ในแผนผังนี้เราเริ่มต้นโดยการกำหนดผู้เรียนรู้ (agent) โดย agent สามารถสำรวจได้ว่าอยู่ที่ไหนของ environment (state) จากนั้น agent สามารปฎิสัมพันธ์กับสิ่งแวดล้อมโดยใช้การกระทำบางอย่าง (action) หลังจากที่ใช้ action ไปแล้ว agent ก็จะได้ reward กลับมา
เราสมมติว่าเวลาในที่นี้เดินแบบไม่ต่อเนื่องคือเริ่มจาก \(t = 1, 2, 3, …\) นั่นเอง ในกรณีที่ถ้าเราเป็นน้องหมา สิ่งที่เราต้องทำอย่างแรกคือลองสังเกตว่า ในที่นี้เราจะเรียกว่า state (\(S\) โดย \(S_0\) หมายถึง state ของน้องหมา ณ เวลา \(t = 0\) นั่นเอง โดยในเวลานี้น้องหมาสามารถออกคำสั่งได้หนึ่งอย่าง (\(A_0\))เช่น ร้องขอข้าว นั่ง กลิ้ง เป็นต้น หลังจากน้องหมาออกคำสั่งไปเรียบร้อย ก็จะได้รางวัลหรือคะแนนกลับมา ในที่นี้คืออาหารเป็นต้น \(R_1\) และเวลาก็จะเลื่อนไปเป็น \(t = 1\) เป็นแบบนี้ไปเรื่อยๆ
ถ้าสมมติว่าน้องหมาคิดว่าการได้กินข้าวคือการได้คะแนนจนกระทั่งน้องหมาแก่ตาย เราจะเขียนลำดับของการทำงานของน้องหมาได้ประมาณนี้
\[S_0 A_0 R_1 S_1 A_1 \ldots R_T S_T\]ถ้า \(t\) ของเรามีจำกัดเช่นจาก \(t = 1, …, T\) เราจะเรียกว่า Episodic task ยกตัวอย่างเช่น การเราจำลองเกมที่เมื่อเก็บเหรียญทั้งหมดครบถือเป็นอันจบด่าน หรือถ้าในเกมไพ่ Blackjack ถ้าไพ่หมดกองก็ถึงว่าจบหนึ่งตา ในกรณีที่ \(t\) สามารถมีค่าเพิ่มไปเรื่อยๆไม่สิ้นสุด เช่นอาจจะเป็นราคาของ Bitcoin, ราคาหุ้น ที่มีค่าใหม่มาเรื่อยๆทุกเวลา เราจะเรียกว่า Continuous task
จะเห็นว่าการทำงานของแผนผังที่เราเล่าไปข้างต้น มีลำดับดังต่อไปนี้
- สังเกตว่าตัวเองอยู่ในสภาวะใด (state)
- ออกคำสั่ง (action)
- ได้ผลลัพธ์หรือคะแนน (reward)
เราเรียกโจทย์นี้อีกชื่อนึงว่า Finite Markov Decision Process (MDP) ซึ่งเป็นโจทย์ของปัญหา Reinforcement Learning ที่เราต้องการจะแก้นี่เอง โดยสิ่งที่เราต้องการนั่นคือการที่ได้ผลลัพธ์ที่ดีที่สุดในตอนท้าย โดยการจะทำให้ได้ผลลัพธ์ที่ดีที่สุดเราสามารถทำได้โดยการหาชุดคำสั่ง (policy) ที่ดีที่สุดในแต่ละ state ที่เราอยู่ ถ้าเขียนเป้นสมการคณิตศาสตร์ก็คือคำสั่งที่นำพา state \(S\) ไปยัง action \(A\) นั่นเอง
\[\pi: S \rightarrow A\]Policy \(\pi\) สามารถเป็นชุดคำสั่งที่เราเขียนขึ้นเอง (deterministic) หรือใช้ความน่าจะเป็นก็ได้ (stochastic) โดยในกรณีของน้องหมาสิ่งที่เราควรทำคือฟังคำสั่งของเจ้าของเพื่อให้ได้อาหารมากที่สุด หรือในกรณีของการเล่น Blackjack เราก็ต้องการได้เงินมากที่สุดก่อนที่จะหมดรอบของการแข่ง (เลือกว่าจะหยิบไพ่เพิมหรือไม่หยิบ) เป็นต้น
ถ้าพอเข้าใจโจทย์กันแล้ว คำถามถัดไปคือ การหาชุดคำสั่งที่ดีที่สุด เราต้องทำยังไงนะ? ในหัวข้อต่อไปเราจะมาพูดถึงการหาชุดคำสั่งที่ดีที่สุด (Optimal Policy) โดยใช้วิธี Monte Carlo และ Temporal Difference (Sarsa, Q-learning) กันฮะ
หา Optimal Policy โดยใช้วิธี Monte Carlo
ในหัวข้อนี้เราจะมาคุยกันว่าเราจะสามารถหาชุดคำสั่งที่ดีที่สุดในแต่ละสถานะที่เราอยู่ได้ยังไงนะ เราไม่สามารถหาชุดคำสั่งที่ดีที่สุดได้ในทันที แต่วิธีหนึ่งในการหาชุดคำสั่งที่ดีที่สุดคือการลองผิดลองถูกและทำให้ดีขึ้นในครั้งหน้านั่นเอง
เพื่อความง่ายต่อการเข้าใจเราจะยกตัวอย่างของการเดินในตารางก่อน โดยเราจะเห็นว่าโลกของเรามีแค่ 4 states เท่านั้น (1, 2, 3, 4) ซึ่งแทนตาราง (ซ้ายล่าง, ซ้ายบน, ขวาล่าง, ขวาบน) ตามลำดับ ส่วนทิศทางการเดินก็ไปได้คือ (ซ้าย, บน, ขวา, ล่าง) โดยเราจะให้ agent เริ่มต้นจาก state 1 (ซ้ายล่าง) และพยายามไปให้ถึง state 4 (ขวาล่าง) เป้าหมายคือเราอยากจะหาชุดคำสั่งของแต่ละ state ที่ทำให้เราได้คะแนนมากที่สุดตอนถึงจุดสุดท้ายนั่นเอง จะเห็นว่าถ้าเรายิ่งเดินผิดมากเท่าไหร่ ก็จะยิ่งอยู่ใน Grid นานกว่าเดิมและคะแนนลดลงเรื่อยๆ
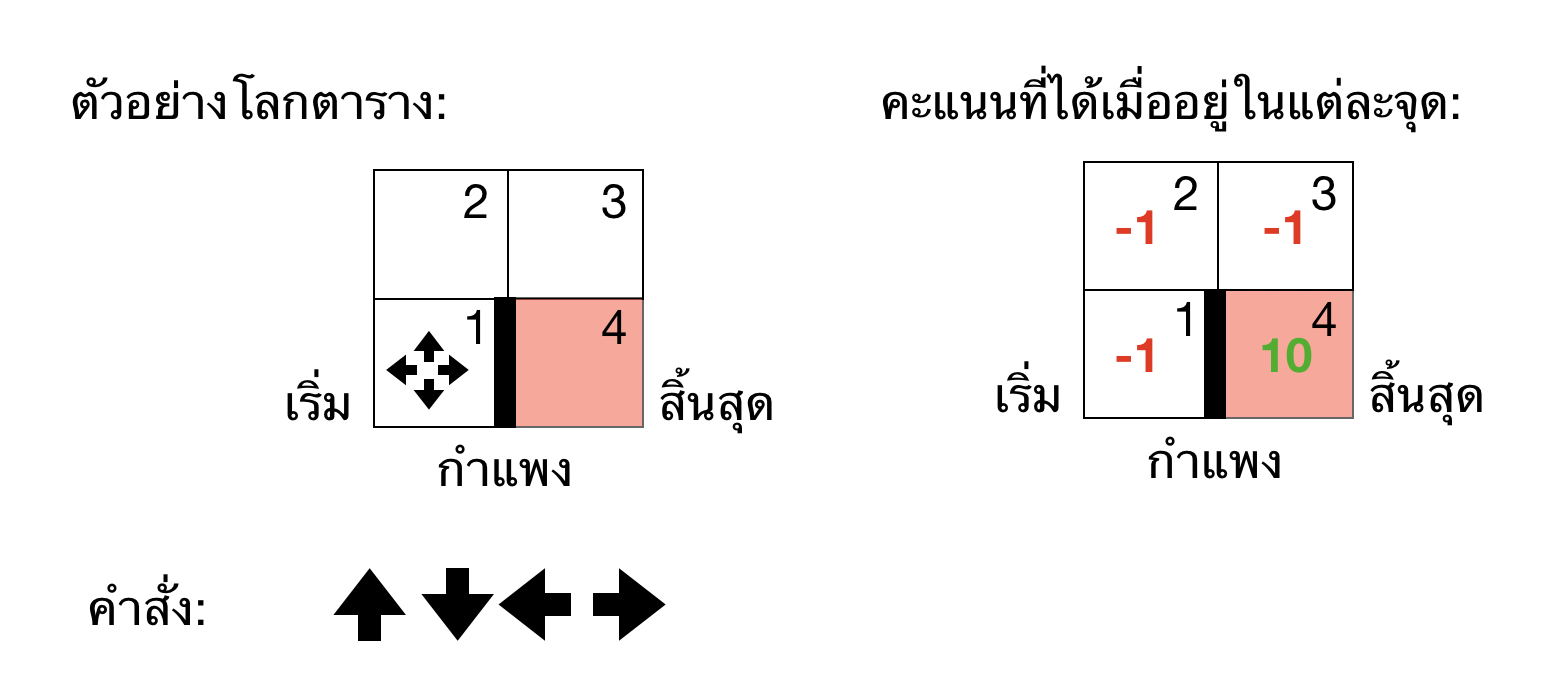
การที่เราจะเดินให้ถูกทาง สิ่งที่เราทำได้คือการประมาณค่าของรางวัลที่เราจะได้เมื่อใช้ action ใน state ที่เราอยู่ให้ได้นั่นเอง ถ้าเราสามารถประมาณค่าเหล่านี้สำหรับทุกรูปแบบของ state กับ action ซึ่งมีชื่อเรียกว่า Q-table หรือตารางที่ประมาณค่ารางวัลของ state และ action ยิ่่งเราประมาณค่าในตารางได้ดีเท่าไหร่ เราก็จะรู้ได้ว่าเราควรจะใช้ action ไหนเมื่ออยู่ใน state ที่เราอยู่ เช่นในกรณีของ Grid ที่เราจำลองขึ้นมา เมื่อเราอยู่ที่ state 1 เราก็ควรจะเดินขึ้นถึงจะเข้าไปใกล้จุดหมายให้ได้เร็วสุดเพราะถ้าเดินไปทางขวาจะติดกำแพง และเดินไปทางซ้ายก็ไม่มีอะไรเกิดขึ้น หรือถ้าเราอยู่ state ที่ 3 เราก็ควรจะเดินลงถึงจะดีที่สุด
การประมาณ Q-table ทำได้หลายวิธีมากๆ โดยวิธีพื้นฐานที่สุดใช้วิธี Monte Carlo โดยวิธีนี้เราทำได้โดยการสร้าง agent ขึ้นมาพร้อมกับ Q-table เริ่มต้น จากนั้นเราจะให้สุ่ม agent เดินไปจนถึงจุดสุดท้าย แล้วอัพเดท Q-table โดยใช้จากรางวัลที่ได่ในตอนท้าย ในหัวข้อข้างล่างเราจะมาดูกันว่า Q-table ถูกอัพเดทอย่างไร
อัพเดทตารางระหว่าง State-Action (Q-table)
อย่างที่กล่าวไปข้างต้น วิธีนี้เราใช้การจำลอง agent ขึ้นมา และให้ agent เดินไปจนถึงจุดสิ้นสุด และอัพเดท Q-table
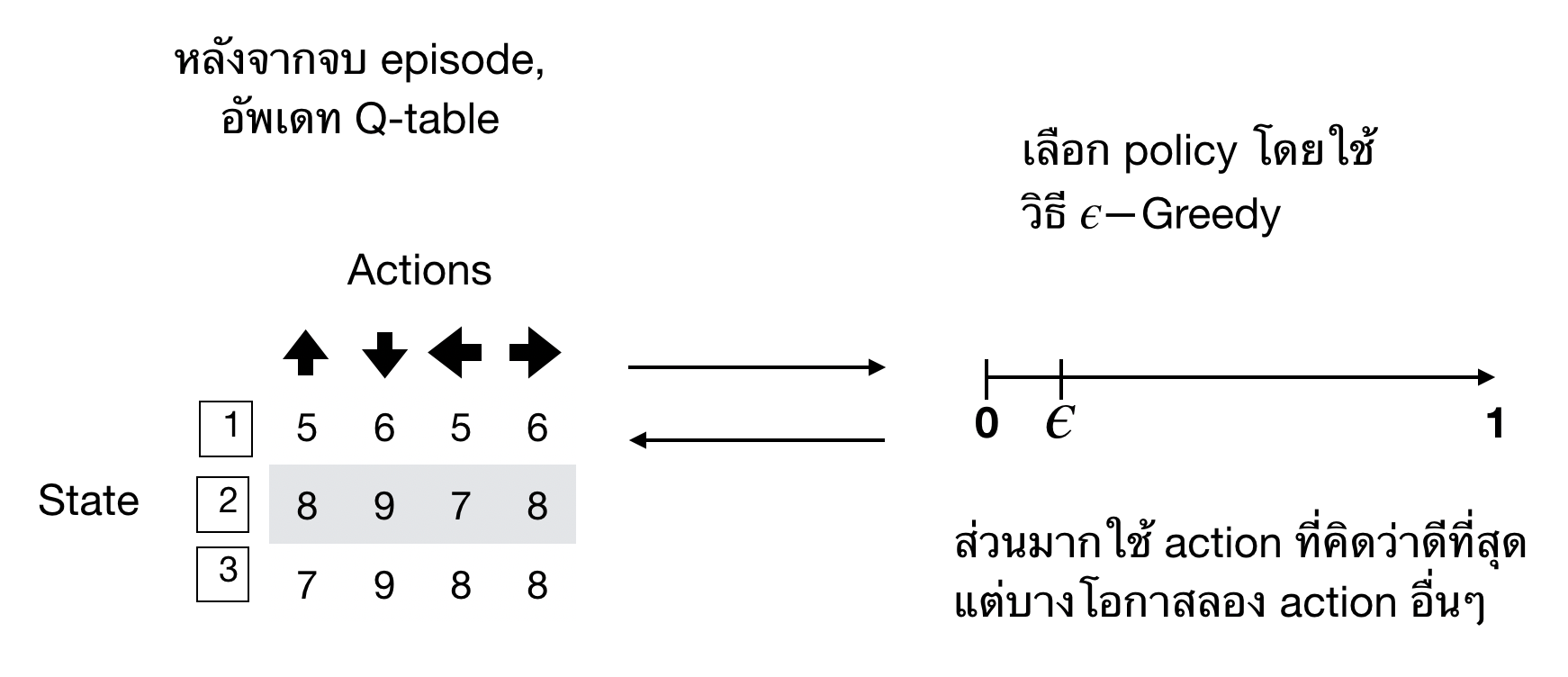
สมการของการอัพเดทเป็นดังนี้
\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (G_t - Q(S_t, A_t))\]โดย \(G_t\) คือรางวัลหรือคะแนน (reward) ที่เราได้ตอนจบ episode หลังจากออกใช้ action นั้นๆไป จะเห็นว่าถ้าหลังจากใช้ action ไปแล้วเราได้คะแนนน้อย ค่า Q ใน state และ action นั้นๆก็จะลดลง แต่ถ้าเราได้คะแนนกลับมามากขึ้น ค่า Q ก็จะเพิ่มมากขึ้นนั่นเอง
สุ่มชุดคำสั่งโดยใช้วิธี \(\epsilon\)-Greedy
จะเห็นว่า Q-table ช่วยให้เราตัดสินใจว่าเราควรจะไปทางไหนได้ แต่ว่า Q-table ที่เราได้มาตอนแรกอาจจะไม่ดีที่สุดก็ได้ ในบางครั้ง action บางอย่างอาจจะทำให้ได้ reward มากกว่า เพราะฉะนั้นเราต้องการเผื่อความน่าจะเป็นไว้เล็กน้อยสำหรับที่จะใช้ action ที่เราไม่เคยใช้มาก่อนในบางที เทคนิคการเลือกชุดคำสั่งแบบนี้เรียกว่า \(\epsilon\)-Greedy คือเราเผื่อความน่าจะเป็น \(\epsilon\) สำหรับการใช้ชุดคำสั่งอื่นๆไว้นั่นเอง
หาชุดคำสั่งที่ดีที่สุดโดยใช้วิธี Temporal Difference Learning
จะเห็นว่าข้อเสียหลักๆของวิธี Monte Carlo ก็คือว่ากว่าเราจะอัพเดท Q-table หรืออัพเดทชุดคำสั่งใหม่นั้น เราจะต้องจำลองสถานการณ์จากเริ่มต้นจนจบ (จบ episode) ถึงจะสามารถอัพเดท Q-table และหาชุดคำสั่งที่ดีกว่าเดิมได้ ในกรณีนี้ต้องใช้เวลาและเปลืองทรัพยากรนานมากๆกว่าเราจะได้ Q-table ที่ดีที่สุด ในกรณีของเกมบางเกมเช่นหมากรุก โกะ หรือเกมที่เราออกแบบ กว่าจะเล่นจนจบ episode ต้องใช้จำนวนครั้งเยอะมากๆ ดังนั้นวิธี Monte Carlo จึงไม่เหมาะสมกับการหา Q-table ที่การจำลองอาจใช้เวลานานมากๆ
แต่ไม่เป็นไรฮะ ความเจ๋งก็คือเราสามารถอัพเดท Q-table ได้ในทันทีหลังจากเราได้ reward กลับมาและย้ายไปอีก state นึง โดยไม่จำเป็นต้องรอให้จบ episode ถึงจะอัพเดท วิธีต่อไปนี้ก็คือ Temporal Difference (TD) Learning โดยเทคนิคที่เป็นพื้นฐานของ TD Learning คือ Sarsa learning และ Q-learning นั่นเอง ลองไปดูกันว่าสองวิธีนี้อัพเดทค่า \(Q(S_t, A_t)\) อย่างไร
Sarsa learning
วิธีนี้ เราสามารถอัพเดทค่า Q แบบนึงหลังจากเราออกคำสั่งไปและอยู่ใน state ถัดไป หลังจากที่เราอยู่ใน state ใหม่แล้วใช้ action เรียบร้อย หรือเราได้ผ่านประสบการณ์หน้าตาประมาณนี้ state-action-reward-state-action (Sarsa) เราจะใช้รางวัลที่เราพึ่งได้มาอัพเดทค่า Q ของ state และ action ที่เราพึ่งผ่านมาได้ตามนี้
\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t))\]Q-learning (Sarsa-max learning)
จะเห็นว่าจาก Sarsa learning จริงๆแล้วเราไม่ต้องรอจนกระทั่งเราออก action ในเวลาถัดไปด้วยซ้ำ เราสามารถใช้ค่าสูงสุดของรางวัลที่เราคิดว่าจะได้ใน state ถัดไปได้เลย ซึ่งสามารถเขียนได้ประมาณนี้
\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (R_{t+1} + \gamma \max_{a \in A} Q(S_{t+1}, a) - Q(S_t, A_t))\]ข้อดีก็คือว่าเราไม่จำเป็นต้องรู้ก็ได้ว่า action ถัดไปจะให้คะแนนเราเท่าไหร่ แค่รู้ว่า action ที่เราพึ่งทำไปทำให้คะแนนเพิ่มขึ้นก็พอแล้ว
ตัวอย่าง
พูดมาซะเยอะ อาจจะเข้าใจยากไปหน่อย เราลองมาดูกันว่าถ้าเรามีชุดคำสั่ง (policy) ที่เกิดขึ้นในเวลานึง เราจะอัพเดทค่า q ใน Q-table อย่างไร

จากตัวอย่างเรามีชุดคำสั่งหน้าตาประมาณนี้ (state 1, ขึ้น, -1, state 2, ขวา) ในเวลานั้นๆเราจะอัพเดทค่า Q อย่างไรโดยการใช้ Sarsa Learning และ Q-Learning?
คำตอบ จะเห็นว่าเราได้ชุดคำสั่ง (state 1, ขึ้น) มา เพราะฉะนั้นเราจะสามารถอัพเดท Q-table ที่ตำแหน่งนั้นได้
- ถ้าใช้ Sarsa ค่า Q จะกลายเป็น
Q(state 1, ขึ้น) = 5 + 0.1 * (-1 + 8 - 5) = 5 + 0.2 = 5.2 - ส่วนถ้าใช้ Q-learning, ค่า Q จะกลายเป็น
Q(state 1, ขึ้น) = 5 + 0.1 * (-1 + max([8, 9, 7, 8]) - 5) = 5 + 0.2 = 5.3แทน นั่นเอง
และถ้าเราทำการอัพเดทไปเรื่อยๆจากการจำลอง agent ก็จะพบว่าค่า Q ของทั้งตารางจะเข้าใกล้ค่าเฉลี่ยของรางวัลที่เราควรจะได้มากขึ้นเรื่อยๆจนใกล้เกือบจุดที่ดีที่สุดนั่นเอง
Reinforcement Learning ใน Continuous Space
จากตัวอย่างข้างบน ผู้อ่านอาจจะคิดว่า โห แล้วในชีวิตจริงมันไม่เหมือนตัวอย่างของ Grid world นี่นา ถ้าเรานึกถึงภาพของหุ่นยนต์ทำความสะอาดในบ้าน เราสามารถมีชุดตัวอย่างของ state มากกว่าแค่ใน Grid world (ซ้ายล่าง, ซ้ายบน, ขวาล่าง, ขวาบน) แต่เป็นตำแหน่งที่หุ่นยนต์ทำความสะอาดในห้อง หน้าตาอาจจะเป็น (0.1 เมตร, 0.3 เมตร), (0.2 เมตร, 0.5 เมตร) จากจุดเริ่มต้นแทน ซึ่งตำแหน่งเหล่านี้อาจจะมีค่าเท่าไหร่ก็ได้ มีคู่ของตำแหน่งให้เลือกไม่สิ้นสุด
เราสามารถแก้ปัญหาใน Continuous Space ได้สองวิธีหลักๆดังนี้
- Discretization หรือการแบ่ง continuous state space ให้เป็นช่วงๆ
- Function Approximation หรือใช้ฟังก์ชันประมาณ state value \(\hat{v}(s) \) และ action value \(\hat{q}(s, a)\) โดยตรง
วิธีที่ง่ายที่สุดที่ทำให้เราสามารถใช้เทคนิคที่เพิ่งคุยกันไปมาใช้ก็คือการแบ่ง continuous state space เป็นช่วงๆหรือการ discretization นั่นเอง เราสามารถแบ่งช่องยิ่งเล็กก็จะยิ่งประมาณ continuous space ได้ดีขึ้น แต่ข้อเสียก็คือว่าขนาดของ Q-table ที่เราต้องสร้างก็จะใหญ่ขึ้นไปอีก และเมื่อ Q-table มีขนาดใหญ่มากๆ ก็อาจจะอัพเดทได้ไม่ทั่วถึงนั่นเอง
ยังมีอีกหลายวิธีที่เราสามารถแทนตำแหน่งใน continuous space ด้วยมิติที่มีขนาดน้อยกว่าพิกัดจริงๆ เช่น การวาดวงกลมหลายๆวงไปบนพื้นผิว แล้วแทนตำแหน่งด้วยวงกลมที่ agent อยู่ แต่ถึงอย่างไรเราก็ต้องกำหนดขนาดของวงกลม กำหนดระยะการซ้อนและอีกหลายปัจจัย ซึ่งต้องใช้ความรู้พื้นฐานถึงจะออกแบบได้ดี
อีกวิธีนึงที่เราสามารถทำได้คือการประมาณฟังก์ชัน state value \(\hat{v}(s) \) และ action value \(\hat{q}(s, a)\) นั่นเอง ในกรณีนี้ก็ไม่ต้องใช้การแบ่ง continuous space เป็นช่วงๆแบบเดิม จะเห็นว่าสิ่งที่เราต้องใส่เพิ่มขึ้นมาขึ้นพารามิเตอร์ \(W \) ที่ใช้สำหรับ map ฟังก์ชันจาก \(s\) ไปเป็น \(v\) และ \((s, a)\) ไปเป็น \(q\)
ในกรณีที่เราเขียนฟังก์ชันเส้นตรง: \( \hat{v}(s, W) = X(s)^T W_{v} \) และ \( \hat{q}(s, a, W) = X(s, a)^T W_{q} \) หรือถ้าเป็นฟังก์ชันไม่เชิงเส้น (nonlinear) ก็จะได้หน้าตาประมาณนี้: \( \hat{v}(s, W) = f_v(X(s)^T W_{v}) \) และ \( \hat{q}(s, a, W) = f_q(X(s)^T W_{q}) \) ซึ่งฟังก์ชัน \(f(.)\) ในที่นี้เราอาจจะเลือกใช้ Neural Network มาช่วยในการประมาณฟังก์ชันไม่เชิงเส้นที่เรามีนี่เอง ตัวอย่วงของการใช้ Neural Network มาประมาณฟังก์ชันได้แก่ Deep Q-Network หรือ DQN ที่จะพูดในหัวข้อถัดไป
Deep Q-Network (DQN)
แน่นอนว่าการแบ่ง state space เป็นช่วง (discretization) สามารถประยุกต์มาใช้แก้ปัญหาที่มีขนาดใหญ่ประมาณนึงได้ แต่เมื่อขนาดของ state เริ่มเป็นไปได้หลายรูปแบบและใหญ่มากขึ้น การใช้เทคนิคการแบ่งช่วงอาจจะทำได้ไม่ง่ายนัก ด้วยประเด็นนี้นี่เองที่ Deep Neural Network จึงถูกนำมาใช้นั่นเอง ข้อดีของ Deep Neural Network คือมันสามารถประมาณฟังก์ชั่นสำหรับ state ได้ในความซับซ้อนที่สูงการฟังก์ชันทั่วไป ซึ่งทำให้เราสามารถประมาณฟังก์ชั่นจาก state ที่มีหลายมิติไปยัง action ได้โดยไม่ต้องใช้การคำนวณหา Q-table เลย
หลายคนอาจจะเคยเห็นโมเดลเหล่านี้จากหลายปีที่ผ่านมา เช่น Deep Q-Network (DQN) ที่สร้างโดย Google Deepmind โดย DQN สามารถเล่นเกม Pong ได้เก่งกว่าคนซะอีก พื่นฐานของ DQN ก็คือการนำ Convolutional Neural Network มาทำความเข้าใจภาพของเกม Pong ขนาด 84 x 84 pixels และพยายามหา action ที่ดีที่สุดโดยใช้เทคนิค Q-learning นั่นเอง ในโพสต์หน้าๆเราจะมาลงรายละเอียดของ Deep Q-Network กัน
ตัวอย่างของ Environments
พูดมาตั้งเยอะแยะ ผู้อ่านคงคิดว่านี่แต่ละครั้งเราต้องไปเขียน environment แล้วยังต้องเขียน agent เพื่อใช้แก้ปัญหาอีกหรอเนี่ย ก็ต้องบอกเลยว่าตอนนี้มีเครื่องมือมากมายที่ช่วยให้เราเขียน environment ขึ้นมาเพื่อลองใช้ Reinforcement Learning แก้ปัญหาได้อย่างไม่ยากนัก อย่าง Unity ก็ออก game engine ให้เราสามารถเขียนเกมมาเพื่อลอง agent ของเราได้ด้วย
Open source สองอันที่คนใช้เป็นจำนวนมากที่มี environment ที่สร้างไว้เรียบร้อย แล้วเราสามารถลองเขียน agent ของตัวเองได้แก่ gym ที่เขียนโดย OpenAI และ ml-agents ที่เขียนโดย Unity ทั้งสองโปรแกรมนี้ได้เขียนขึ้นมาโดยเราสามารถเรียก environment และ agent ขึ้นมาได้อย่างไม่ยากนัก ยกตัวอย่างเช่น gym ก็มี environment ของเกมไพ่อย่าง Blackjack และ Cartpole ที่เราต้องพยายามพยุงไม้บนรถที่เลื่อนในสองมิติให้ได้
สำหรับ gym นั้น มาพร้อมกับ environment เกือบ 100 แบบที่สามารถให้เราลองแก้ปัญหาได้ และ ml-agents มาพร้อมกับ Unity Hub ซึ่งนอกจากเราจะสามารถใช้เกมที่มีอยู่ทั่วไปแล้ว ยังสามารถลองเขียนเกม
(environment) ใหม่ๆพร้อมกับ agent และ action ได้อีกด้วย
ตัวอย่างของโค้ดในการสร้าง environment โดยใช้ไลบรารี่ gym
import gym
env = gym.make('Blackjack-v0')
print(env.action_space) # Discrete(2): hits (ขอไพ่เพิ่ม), sticks (ไม่ขอไพ่เพิ่ม)
observation = env.reset() # เริ่มดูไพ่
print(done) # จบตาแรก
action= env.action_space.sample() # สุ่ม action (hits/ sticks)
observation, reward, done, info = env.step(action)
print(done) # จบเทิร์น
และการสร้าง environment โดยใช้ไลบรารี่ mlagents ยกตัวอย่างเช่นเกมเก็บกล้วยของ Unity
from mlagents.envs.environment import UnityEnvironment
env = UnityEnvironment(file_name="/Banana_Linux_NoVis/Banana.x86_64")
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
env_info = env.reset(train_mode=True)[brain_name]
print(env_info.agents) # number of agents = 1
print(brain.vector_action_space_size) # action size = 4 (w,a,s,d) => ขึ้น,ซ้าย,ลง,ขวา
prtin(len(env_infor.vector_observations)) # dimension of states = 37
เมื่อเราสร้าง environment ขึ้นมาแล้ว เราสามารถทดลอง
สรุป
ในบล็อกนี้เราได้เรียนรู้กับ Reinforcement Learning โดยยกตัวอย่างของ Grid world เข้ามาเพื่อทำความเข้าใจกับการหา Q-table โดยใช้วิธี Monte Carlo และ Temporal Difference เราพูดต่อไปว่าใน Continuous Space เราไม่สามารถใช้ Q-table ได้เนื่องจากคาวมเป็นไปได้ของ State มีจำนวนไม่จำกัด เราสามารถแก้ปัญหาโดยใช้การแบ่งช่วงของ Continuous space ให้มีจำนวนน้อยลงเพื่อใช้ Q-table ได้ (discretization) หรือเราจะเลือกใช้ Deep Neural Network มาประมาณฟังก์ชันระหว่าง state กับ action เพื่อหาชุดคำสั่งก็ได้ เป็นที่มาของ Deep Reinforcement Learning นั่นเอง
ในโพสต์นี้เรายังไม่กล่าวถึง Policy agent และ Multi-agent Learning โดยเราจะเขียนเพิ่มเติมในโพสต์หน้าๆฮะ รอติดตามในโพสต์หน้าๆฮะ!
