สำหรับโพสต์นี้เราจะพูดถึงแอพที่เราใช้ฟังเพลง มีชื่อว่า Spotify และนอกจากนั้นก็จะพูดถึง ฟีเจอร์การแนะนำเพลงรายสัปดาห์ของ Spotify ที่มีชื่อว่า Discover Weekly และเบื้องหลังการแนะนำเพลงว่า เค้าทำกันยังไงนะ เราจะปิดท้ายด้วยการลองเขียน Collaborative Filtering (หรือเทคนิกที่เรียกว่า non-negative matrix factorization) อย่างง่ายโดยใช้โปรแกรมภาษา Python อีกด้วย
ใครที่สนใจมากกว่านี้ ก็สามารถอ่านบทความที่เกี่ยวข้องได้ตามลิงค์ด้านล่างเลยนะ
- Albert Au Yeung, Matrix Factorization: A Simple Tutorial and Implementation in Python
- Chris Johnson, Algorithmic Music Recommendations at Spotify
- Ben Popper, TASTEMAKER, How Spotify’s Discover Weekly cracked human curation at internet scale
การหาเพลงฟังใหม่
ถ้าใครเป็นเพื่อนเราใน Facebook จะสังเกตได้ว่า เราเป็นคนที่ชอบฟังเพลงมากๆ การฟังเพลงนี่ถือได้ว่าเป็นงานอดิเรกหลักของวันเลยแหละ ในสัปดาห์นึงนี่จะมีวันที่ต้องหาเพลงใหม่ๆมาฟัง ส่วนเพลงที่ชอบก็จะโพสต์ลงไปบนวอล์บ้าง ซึ่งส่วนมากก็ไม่ค่อยมีใครฟังเท่าไหร่หรอก แต่ก็ชอบกลับมาหาเพลงที่ตัวเองโพสต์ฟังเนี่ยแหละ
แต่ข้อเสียหลักๆของการหาเพลงฟังด้วยตัวเองก็คือว่า เรามักจะวนกลับมาฟังวงเดิมๆในที่สุด หรือไม่ก็ยังฟังแนวเดิมๆตามเพจที่เราฟังอยู่เรื่อยๆ ดังนั้นก็ต้องหาทางเพื่อที่จะเจอกับเพลงใหม่ๆบ้าง
การหาเพลงใหม่ๆฟังก็ไม่ได้ง่ายเพราะมีคนฟังแนวเดียวกับเราค่อนข้างน้อย มีเพียงไม่กี่คนที่ฟังเพลงแนวใกล้ๆกัน บางทีก็ไปฟังตามเพจบน Facebook เช่น อินดี้สมัยใหม่ หรือทางสุดท้ายก็ไปฟังบน Youtube ซึ่งเรา subscribe แชนแนลที่ชอบๆไว้ เช่นพวก Pitchfork, IndieAir เป็นต้น
Spotify
นอกจากเพจหรือ Youtube ที่เราใช้ตามฟังเพลงแล้ว Spotify ถือเป็นอีกตัวเลือกที่แนะนำเพลงใหม่ๆที่เราไม่เคยฟังได้ดีพอสมควรเลย แต่ก่อนที่จะพูดถึงการแนะนำเพลง เรามาทำความรู้จักกับ Spotify ซักเล็กน้อย
Spotify เป็นบริษัทซึ่งให้บริการ stream เพลง เช่นเดียวกับ Google Play Music, Apple Music หรือ Deezer ซึ่งบริษัทแม่ตั้งหลักปักฐานอยู่ที่มหานครนิวยอร์ก ในสหรัฐอเมริกา สำหรับคนที่ไม่เคยใช้ก็สามารถโหลด Spotify แล้วก็ฟังเพลงได้ฟรีๆเลย แต่อาจจะมีโฆษณาคั่นระหว่างเพลงบ้าง ถ้าคนที่ไม่ต้อการฟังโฆษณาก็สามารถจะเลือกจ่าย 5 เหรียญสหรัฐต่อเดือนเพื่อเป็นสมาชิกและเอาโฆษณาออกก็ได้ นอกจากนั้น การเป็นสมาชิกสามารถดาวน์โหลดเพลงมาเล่นบนมือถือแบบ offline ได้อีกด้วย
ในหน้าหลักของแอพพลิเคชั่นเรายังสามารถเข้าไปฟังลิสต์เพลงที่มีคนคัดมาให้แล้วได้ด้วย เช่น รูปข้างล่างคือลิสต์รวมเพลง Sexiest K-Groove จาก Spotify เป็นต้น
เหนือไปกว่านั้น Spotify มีฟีเจอร์ที่เจ๋งมากๆอีกอย่างที่เรากำลังจะพูดต่อไปในโพสต์นี้ซึ่งเป็นฟีเจอร์การแนะนำเพลงรายสัปดาห์หรือ Discover Weekly นั่นเอง
Discover Weekly และ Collaborative filtering
สำหรับคนที่ใช้ Spotify เมื่อเราโหลด Spotify มา ในสัปดาห์แรก Spotify เป็นแอพทั่วไปที่เราใช้ฟังเพลง เราก็ฟังเพลงยาวๆไปประมาณหนึ่งสัปดาห์ จะฟังเพลงจากวงที่เราฟังเป็นปกติบน Youtube หรือเพลงอะไรที่ชอบก็ได้ มั่วๆไป แต่เมื่อผ่านไปหนึ่งสัปดาห์ Spotify ก็จะมีแถบแนะนำเพลงใหม่ประจำสัปดาห์ขึ้นมาที่ชื่อว่า Discover Weekly โดยประมาณแล้วเพลงทั้งหมดที่แนะนำจะมีความยาวประมาณ 1.5 ถึง 2 ชั่วโมง ซึ่งโดยส่วนตัวของเราแล้ว เพลงที่ Spotify แนะนำแต่ละสัปดาห์เรียกได้ว่าเจ๋งมากๆ บางวงหรือบางเพลงไม่เคยได้ยินมากก่อนเลยด้วยซ้ำ แต่เพลงนี่มันใกล้เคียงกับที่เราฟังมากสุดๆ คนที่มี Spotify คงเข้าใจได้ว่าฟีเจอร์นี้มันเจ๋งขนาดไหน
หลักการทำงานของการแนะนำเพลงโดยคร่าวๆนั้น เค้าใช้ข้อมูลจากการฟังเพลงของเราเมื่อสัปดาห์ที่ผ่านมา แล้วเอาแพทเทิร์นการฟังเพลงนั้น ไปเปรียบเทียบกับคนที่ฟังเพลงคล้ายๆกัน แล้วแนะนำเพลงเราไม่เคยฟังมาก่อนแต่เราน่าจะชอบให้เราฟัง
ดังที่กล่าวไปในตอนต้น อัลกอริทึมที่ Spotify ใช้มีชื่อว่า Collaborative Filtering นั่นเอง โดยเทคนิกนี้พื้นฐานของการประมาณเมทริกซ์ที่เรียกว่า Non-Negative Matrix Factorization
Collaborative Filtering คืออะไร?
Collaborative Filtering เริ่มได้รับความสนใจเป็นอยากมากเนื่องจากคนที่คิดอัลกอริทึ่มได้ดีที่สุดในปีนั้นๆ จะได้รางวัล Netflix price ไป
เราจะพูดถึง Netflix และ Netflix price ก่อนแล้วกัน Netflix เป็นบริการ stream หนังรายใหญ่ของอเมริกา ว่าได้ว่า ชาวมะกันจะต้องมีบริการนี้ไว้ใช้ดูหนังทุกเวลายามว่างเลยทีเดียว ผู้ใช้งาน Netflix จะสามารถเรตคะแนนหนังแต่ละเรื่องได้เป็นจำนวนดาว 0-5 ดาว
สำหรับ Netflix สิ่งที่เค้าต้องการก็คือเค้าต้องการประมาณว่าผู้ใช้งานจะเรตหรือให้คะแนนกับหนังมากเท่าไหร่ โดยดูจากการให้คะแนนหนังที่ผ่านๆมาของผู้ใช้งานคนนั้นๆ โดยการเทียบกับผู้ใช้งานที่มีลักษณะคล้ายๆกัน ถ้าหนังเรื่องนั้นมีโอกาสจะได้ดาวมากจากผู้ใช้งาน Netflix ก็จะได้แนะนำหนังเรื่องนั้นให้ผู้ใช้ได้นั่นเอง
ยกตัวอย่างเช่น เราที่ชอบดูหนัง sci-fi แต่ไม่ชอบดูหนังรัก เราก็มีโอกาสจะให้คะแนนหนัง เช่น Star War หรือ Star Trek มากกว่า 500 days of Summer ดังนั้นถ้าหนังเรื่องใหม่เข้ามา เช่น Interstellar, Netflix สามารถเทียบเรากับผู้ใช้งานคนอื่นที่ให้คะแนนหนัง Interstellar และมีรสนิยมการดูหนังคล้ายๆเรา แล้วเดาได้ว่าเราจะให้คะแนน Interstellar มากขนาดไหน
สำหรับ Spotify Discover Weekly ก็คล้ายคลึงกัน แต่ในกรณีของ Spotify เค้าต้องการจะแนะนำเพลงที่ เราอยากฟัง โดยเทียบเรากับผู้ใช้งานคนอื่นๆบน Spotify นั่นเอง
Collaborative Filtering ทำงานอย่างไร?
อารัมภบทมาซะเยอะเลย ต่อไปเราจะมาดูกันว่า Collaborative filtering นี่มันทำงานยังไง
เริ่มต้นจากข้อมูลของเราก่อน สมมติว่าเรามีเซ็ตของผู้ใช้งาน \(U\) (users) โดยมีขนาด \(n\) คน และมีเซ็ตของเพลง \(D\) (songs) ซึ่งมีขนาด \(m\) เพลง นอกจากนั้น สมมติว่าเรามีประวัติการฟังเพลงสัปดาห์ที่ผ่านมาของแต่ละผู้ใช้งาน ว่าเค้าฟังเพลงแต่ละเพลงไปแล้วกี่ครั้ง
เราสามารถเขียนจำนวนการฟังเพลงของ ผู้ใช้งานทั้งหมดในรูปของเมทริกซ์ได้ โดยเราจะใช้ชื่อว่า \(\mathbf{R} \) ซึ่งมีขนาดเท่ากับขนาดของผู้ฟังทั้งหมดและจำนวนเพลง หรือว่า \(n \times m \) ในแต่ละตำแหน่งของเมทริกซ์ เราจะใช้สัญลักษณ์ว่า \( r_{ij} \) แทนจำนวนครั้งที่ผู้ใช้งาน \(i\) ฟังเพลง \(j\) ส่วนเพลงที่ผู้ใช้ไม่เคยฟัง เราก็ไม่ต้องใส่ข้อมูลใดๆไปบนเมทริกซ์นั้น หรือทิ้งค่าว่างๆไว้เป็น 0 ก็ได้
สิ่งที่เราต้องการจะหาคือเมทริกซ์อันดับต่ำ (low-rank matrix) ที่จะบรรยายทั้งผู้ใช้งานและเพลงที่ผู้ใช้งานฟัง พูดง่ายๆคือว่า เราต้องการหาเวกเตอร์ขนาดไม่ใหญ่มากเพื่อใช้บรรยายการผู้ใช้งาน
\[\begin{equation} \hat{\mathbf{R}} = \mathbf{P} \times \mathbf{Q}^T \approx \mathbf{R} \end{equation}\]โดยที่ \(\mathbf{P}\) มีขนาด \(n \times k \) และ \(\mathbf{Q}^T\) มีขนาด \(k \times m \). สิ่งที่เราต้องการคือเราสามารถประมาณเมทริกซ์ \(\mathbf{R}\) ด้วย \(\hat{\mathbf{R}} = \mathbf{P} \times \mathbf{Q}^T\)
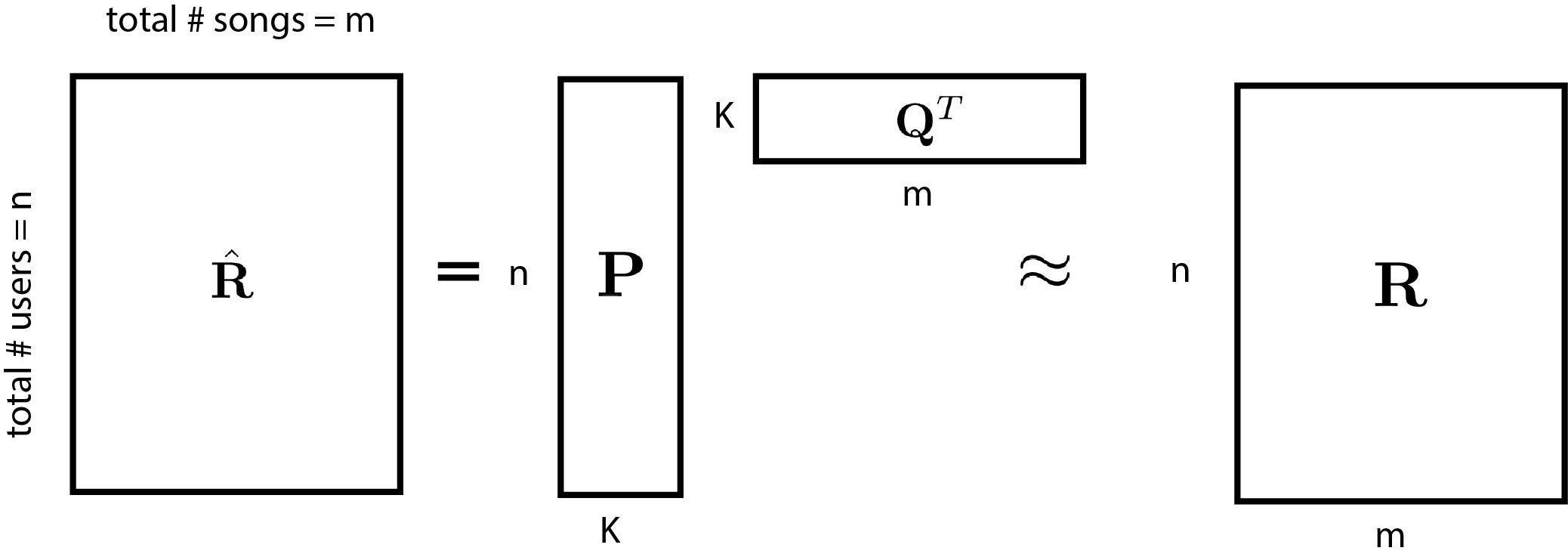
เราจะเห็นว่าเมทริกซ์ \(\mathbf{P}\) มีจำนวนแถวเท่ากับจำนวนผู้ใช้งานเลย ถ้าเรามีเมทริกซ์นี้แล้ว ในแต่ละแถว เราสามารถใช้บอกได้ว่า ผู้ใช้งานคนใดมีลักษณะการฟังเพลงคล้ายๆกัน นอกจากนั้น ถ้าเราเอาแถวนึงจากเมทริกซ์ \(\mathbf{P}\) มาคูณกับเมทริกซ์ \(\mathbf{Q}\) เราจะสามารถบอกได้ว่า ผู้ใช้งานคนนั้นควรจะฟังเพลงอะไรเพิ่มบ้างนอกเหนือจากที่เค้าฟังอยู่ ยกตัวอย่างคะแนนหรือจำนวนเพลงที่ลูกค้าคนที่ \(i\) ควรจะฟังในแต่ละเพลง สามารถคำนวณได้ดังด้านล่าง
\[\begin{equation} \mathbf{\hat{r}}_i = \mathbf{p}_i \times \mathbf{Q}^T \end{equation}\]สิ่งที่เราต้องการจะหาคือทำให้ความผิดพลาดของการประมาณ (\(e_{ij}\) ) ในทุกๆตำแหน่งของ \(\hat{\mathbf{R}}\) เมื่อเทียบกับ \(\mathbf{R}\) มีค่าน้อยที่สุด นั่นคือในแต่ละตำแหน่ง
\[\begin{equation} e_{ij}^2 = (r_{ij} - \hat{r}_{ij})^2 = (r_{ij} - \sum_{k=1}^{K} p_{ik} q_{kj})^2 \end{equation}\]และจากโพสต์ที่แล้วที่ว่าด้วย Gradient descent เราสามารถหาพารามิเตอร์ที่ดีที่สุดได้ด้วยการดิฟค่าความผิดพลาดนี้ เทียบกับพารามิเตอร์ที่เราต้องการจะหา
\[\begin{eqnarray} \frac{\partial}{\partial p_{ik}} e_{ij}^2 & = - 2 (r_{ij} - \hat{r}_{ij}) \times q_{kj} = -2 e_{ij}q_{kj}\\ \frac{\partial}{\partial q_{kj}} e_{ij}^2 & = - 2 (r_{ij} - \hat{r}_{ij}) \times p_{ik} = -2 e_{ij}p_{ik} \end{eqnarray}\]ในบ้างครั้งค่าของการประมาณเมทริกซ์ \(\mathbf{P}\) และ \(\mathbf{Q}\) อาจจะมากเกินไป หรืออาจจะติดลบไปมากๆ ซึ่งเราไม่อยากจะให้เกิดขึ้น โดยส่วนมากแล้ว เราจะใส่สิ่งที่เรียกว่า regularization term เข้าไปด้วยเพื่อทำให้ค่าที่เราประมาณมีขนาดไม่ใหญ่จนเกินไป
\[\begin{equation} e_{ij}^2 = (r_{ij} - \sum_{k=1}^{K} p_{ik} q_{kj})^2 + \frac{\beta}{2} \sum_{k=1}^K (\| p_{ik} \|^2 + \| q_{jk} \|^2 ) \end{equation}\]เกรเดียนท์ที่เราจะใช้ เขียนได้คล้ายๆเดิม ดังต่อไปนี้
\[\begin{eqnarray} \frac{\partial}{\partial p_{ik}} e_{ij}^2 & = - 2 e_{ij}q_{kj} + \beta p_{ik}\\ \frac{\partial}{\partial q_{kj}} e_{ij}^2 & = -2 e_{ij}p_{ik} + \beta q_{kj} \end{eqnarray}\]เราค่อยๆวนไปแต่ทุกๆแถวและหลักของเมทริกซ์ และอัพเดท \(p_{ik}, q_{kj}\) ใหม่ ได้ดังต่อไปนี้
\[\begin{eqnarray} p_{ik} &= p_{ik} - \alpha (- 2 e_{ij} q_{kj} + \beta p_{ik})\\ q_{kj} &= q_{kj} - \alpha (- 2 e_{ij} p_{ik} + \beta q_{kj}) \end{eqnarray}\]ถ้ายังจำได้จากโพสต์ที่แล้วอีกที \(\alpha\) สามารถเรียกได้ว่า learning rate นั่นเอง และ \(\beta\) เป็นค่าที่บอกว่าเราควรจะให้น้ำหนักของ regularization กับพารามิเตอร์มากขนาดไหน
อ่านเลขมากซะเยอะ จริงๆแล้วโค้ดที่ใช้สำหรับประมาณค่าเมทริกซ์ \(\mathbf{P}\) และ \(\mathbf{Q}\) สามารถเขียนได้ไม่ยากมาก ตามด้านล่าง
import numpy as np
def matrix_factorization(R, P, Q, K=2, steps=5000, alpha=0.0002, beta=0.02, tol=0.001):
n, m = R.shape
Q = Q.T
for _ in range(steps):
for i in range(n):
for j in range(m):
if R[i][j] > 0:
eij = R[i][j] - np.dot(P[i,:], Q[:,j])
for k in range(K):
P[i][k] = P[i][k] + alpha * (2 * eij * Q[k][j] - beta * P[i][k])
Q[k][j] = Q[k][j] + alpha * (2 * eij * P[i][k] - beta * Q[k][j])
eR = np.dot(P, Q)
e = 0
for i in range(n):
for j in range(m):
if R[i][j] > 0:
e = e + (R[i][j] - np.dot(P[i,:], Q[:,j])) ** 2
for k in xrange(K):
e = e + (beta/2) * (P[i][k] ** 2 + Q[k][j] ** 2) # total error
if e < tol:
break
return P, Q.T
ยกตัวอย่างง่ายๆ เช่นเรามีผู้ใช้งานทั้งหมด 5 คน และเพลงทั้งหมด 4 เพลง โดยแต่ละตำแหน่งบอกว่า ผู้ใช้งานคนที่ \(i\) ฟังเพลงที่ \(j\) เป็นจำนวนกี่ครั้ง 0 หมายความว่าผู้ใช้คนนั้นไม่เคยฟังเพลงดังกล่าวมาก่อนเลย
R = np.array([[5,3,0,1], # user 1
[4,0,0,1], # user 2
[1,1,0,5], # user 3
[1,0,0,4], # user 4
[0,1,5,4]]) # user 5
n, m = R.shape
K = 2 # latent variable
P = np.random.rand(n, K) # randomly create P, Q first
Q = np.random.rand(m, K)
P, Q = matrix_factorization(R, P, Q, K)
Rhat = numpy.dot(P, Q.T)
เมื่อเราโชว์ค่าของเมทริกซ์ที่ประมาณออกมา จะเห็นว่าได้เป็นประมาณนี้
print(Rhat)
song1 song2 song3 song4
[[ 4.98 2.96 2.97 0.99] # user 1
[ 3.97 2.37 2.59 0.99] # user 2
[ 1.04 0.89 5.72 4.95] # user 3
[ 0.97 0.79 4.63 3.97] # user 4
[ 1.52 1.12 4.92 4.04]] # user 5
เราจะเห็นได้ว่า ตำแหน่งที่เราประมาณ R จาก Rhat มีค่าใกล้เคียงกันมาก และนอกจากนั้น Rhat ยังมี
ใส่ค่าที่ R ไม่มีเข้าไปอีกด้วย ลองเปรียบเทียบผู้ใช้งานคนที่ 4 และ 5 จะเห็นว่าเค้าชอบฟังเพลงที่ 4 เหมือนกัน
แต่เรามีข้อมูลว่า ผู้ใช้งานคนที่ 5 ชอบฟังเพลงที่ 3 ด้วยบ่อยๆ จะเห็นว่าค่าประมาณ Rhat ของอยากจะให้ผู้ใช้งานคนที่ 4
ฟังเพลงที่ 3 เช่นกัน (แนะนำให้ฟัง 4.63 ครั้ง) หรือพูดง่ายๆคือเราควรจะแนะนำเพลงที่ 3 ให้ผู้ใช้คนที่ 4 ฟังนั่นเอง
ส่งท้าย
ตัวอย่างข้างบนเป็นแค่ตัวอย่างเล็กๆเท่านั้น ในความเป็นจริงแล้ว Spotify มีผู้ใช้งานประจำถึง 100 ล้านคน ผู้ใช้งานที่จ่ายเงินกว่า 30 ล้านคน และมีเพลงเกินกว่า 30 ล้านเพลง Collaborative filtering ที่เค้าใช้ มีความซับซ้อนกว่าที่เราอธิบายข้างต้นมากๆ แต่หวังว่าคนที่อ่านโพสต์นี้จะพอเข้าใจวิธีการแนะนำเพลง (และหนัง) ของบริษัทใหญ่ๆในปัจจุบัน สำหรับคนที่สนใจจะต่อยอดก็สามารถเอาไปใช้กับข้อมูลที่ตัวเองมีได้ ไม่ว่าจะเป็นการหาผู้ใช้งานที่มีลักษณะคล้ายคลึงกัน หรือว่าจะใช้แนะนำสินค้าก็ได้นะเออ
สำหรับคนที่อยากจะใช้งานจริงๆจังๆ ลองดู Python library เช่น scikit-learn หรือ pyspark ซึ่ง เขียนโค้ดของ Non-Negative Matrix Factorization กับ Collaborative Filtering ก็ได้นะ
