ทำไมถึงต้องใช้ Causal Inference

By TITIPATA

ชอบฟังเพลงอินดี้และอัลเทอร์เนทีฟ เวลาว่างชอบเขียนโปรแกรมและเล่นเกม

Email Twitter Google+ Github

สัปดาห์ที่ผ่านมาได้เริ่มเรียนวิชาการหาความเป็นสาเหตุ (Causal Inference) กับอาจารย์​คอนราด คอร์ดดิง (Konrad Kording) ที่ University of Pennsylvania ในวิชานี้ตอนเริ่มวิชาคอนราดได้พูดถึงว่าทำไมเราต้องนำ Causal Inference มาใช้ในศาสตร์ประสาทวิทยา (Neuroscience) ไว้ได้ดีมากๆ โดยนำเอาระบบขนาดเล็กมาอธิบายเพื่อให้เข้าใจภาพกว้างของวิชา รู้สึกว่าได้แนวคิดที่เจ๋งมากๆจากตัวอย่างเล็กๆเลยเอามาเขียนแชร์กันฮะ

ในบล็อกนี้เราจะมาพูดถึงกันว่าทำไมเทคนิคอย่างเช่น Functional Connectivity ที่งานวิจัยประสาทวิทยาที่ก่อนหน้าทำกันมาจึงไม่เพียงพอ และทำไมเราจำเป็นถึงต้องใช้เทคนิคอย่างเช่น Causal Inference มาศึกษาวิชาประสาทวิทยาเพิ่มเติม และเราจะพูดปิดท้ายไว้เล็กน้อยเกี่ยวกับวิธีการใช้ Causal Inference จากศาสตร์วิชาต่างๆ

ส่วนรายละเอียดของเทคนิคของ Causal Inference เราจะมาพูดคุยกันในโพสต์หน้าๆ และมาพูดถึงความสำคัญของการนำ Causal Inference มาใช้ในศาสตร์อย่าง Machine Learning หรือ Deep Learning ที่มีความฮิตในปัจจุบันฮะ

ทำไมต้องมี Causal Inference ในวิชา Neuroscience

ในหัวข้อนี้เราจะย้อนกลับไปพูดถึงโมเดลของเซลล์ประสาทหรือ Spiking neurons แบบง่ายๆที่คนใช้กันมาก่อนฮะ เราจะลองมาดูว่าสำหรับระบบเล็กๆเราสามารถเรียนรู้อะไรจากมันได้บ้าง และถ้าระบบมีขนาดใหญ่ขึ้นทำไมการหาความสัมพันธ์อย่างเช่นการสร้างเมทริกซ์ความสัมพันธ์ระหว่างเซลล์ประสาทหรือ Functional Connectivity ทำได้ยาก

เริ่มจากจำลองระบบของเซลล์ประสาทอย่างง่าย

ถ้าเราให้ \(x\) เป็นเวกเตอร์ของเซลล์ประสาทซึ่งมีขนาด \(N \times 1\) โดย \(N\) คือจำนวนเซลล์ประสาทในระบบที่เรามี ปกติแล้วเซลล์ประสาทจะเชื่อมต่อกันด้วยฟังก์ชัน \(f(.)\) และส่วนมากเราจะสมมติว่าเซลล์เหล่านี้เชื่อมต่อกันด้วยความน่าจะเป็นประมาณ 10-20 เปอร์เซ็นต์ เราสามารถเขียนสมการของเซลล์ประสาทในเวลา \(t\) โดย \(t = 0, 1, 2, …\) ได้ดังนี้

โดยปกติ noise หรือสัญญาณรบกวนในระบบเราจะสมมุติว่ามาจาก Gaussian noise นั่นเอง

จากนั้นเราจะสมมุติให้ระบบมีความซับซ้อนน้อยลงไปอีก โดยเราจะสมมุติว่าฟังก์ชั่นนั้นเป็นแบบ linear system โดยเราจะแทน \(f(.) \) ได้ด้วยเมทริกซ์ \(A\) และสามารถเขียนสมการได้ดังนี้

จากนั้นเราจะมาเขียนโค้ด Python เพื่อจำลองระบบโดยให้จำนวนเซลล์ประสาทมีขนาดเท่ากับ 10 เซลล์กัน เราจะสร้างเมทริกซ์ \(A\) ให้เป็นเมทริกซ์ที่ส่วนมาก (90 เปอร์เซ็นต์) มีค่าเท่ากับ 0 (Sparse Matrix) และอีก 10 เปอร์เซ็นต์มีค่า เราจะหารให้เมทริกซ์ด้วย singular value สูงที่สุดให้มันมีความเสถียร ไม่ลู่ออก ลองดูโค้ดได้ตามด้านล่าง

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def create_state_matrix(n_dim=10):
    """
    Create state matrix where we reweight to smaller singular value
    """
    A = np.random.rand(n_dim, n_dim)
    A = (A < 0.1).astype(float) # sparse A matrix
    u, s, v = np.linalg.svd(A) # singular value decomposition
    A = A / (s[0] * 1.01) # reweight matrix so the system is stable
    return A

def simulate_system(A, n_timestep=1000, noise_level=0.5):
    """
    Simulate the system with n_timestep with the given noise level
    """
    n, _ = A.shape
    x_vec = []
    x = np.random.randn(n, 1)
    for _ in range(n_timestep):
        x = A.dot(x) + noise_level * np.random.randn(n, 1)
        x_vec.append(x)
    x_vec = np.hstack(x_vec)
    return x_vec

เราจะเริ่มด้วยการทดลองจำลองโมเดลที่ \(A\) มีขนาด \(10 \times 10\) โดยเราเก็บข้อมูลทั้งหมด 1000 สเต็ปและให้ขนาดของ noise = 0.5 ส่วนการหาความสัมพันธ์ระหว่างเซลล์ประสาทนั้น วิธีที่คนส่วนมากใช้ก็คือการหา correlation ระหว่างสัญญาณประสาทของเวลา \(t\) กับเวลา \(t + 1\) นั่นเอง หรือเราอาจจะเรียกว่า Functional Connnectivity ก็ได้

n_timestep = 1000
noise_level = 0.5
A = create_state_matrix(n_dim=10)
x_vec = simulate_system(A, n_timestep=n_timestep, noise_level=noise_level)

# ประมาณเมทริกซ์ A จากสัญญาณที่เก็บมา
n = x_vec.shape[0]
A_approx = np.cov(x_vec[:, :n_timestep - 1], x_vec[:, 1:], rowvar=1)[n:, 0:n]

ลองมาดูว่า \(A\) กับ \(A_{approx}\) มีหน้าตาเหมือนหรือต่างกันอย่างไร ด้านล่างเลย

plt.subplot(1, 2, 1)
plt.imshow(A)
plt.subplot(1, 2, 2)
plt.imshow(A_approx)
plt.show()
print(np.corrcoef(A.ravel(), A_approx.ravel())) # correlation between 2 matrices

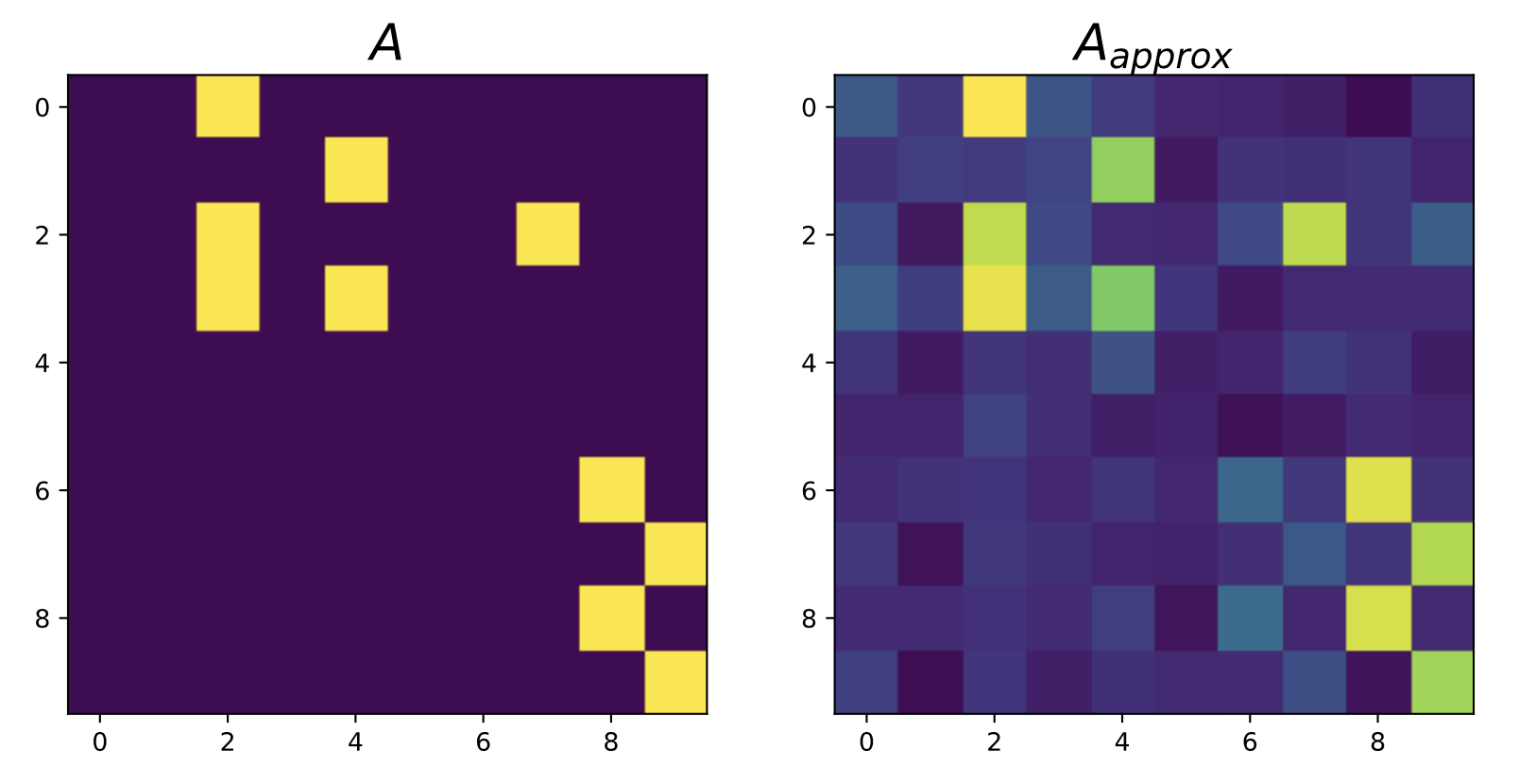
เราจะเห็นว่าถ้าระบบมีขนาดไม่ใหญ่จนเกินไป หน้าตาของ \(A\) กับ \(A_{approx}\) มีความคล้ายคลึงกันมากๆ ถ้าเราหา correlation ระหว่างเมทริกซ์ทั้งสองจะได้ประมาณ 0.924 สำหรับเมทริกซ์ที่เราสุ่มขึ้นมา (correlation อาจจะต่างไปเนื่องจาก \(A\) ได้มาจากการสุ่ม) สรุปได้ว่า ถ้าระบบมีขนาดไม่ใหญ่มากนั้นเราสามารถสรุปได้ว่า Correlation คือ Causation หรือว่าเราสามารถประมาณระบบได้จากสัญญาณที่เก็บมาได้

เราลองจำลองระบบขึ้นมาอีกครั้งโดยที่ขนาดของ \(A\) กลายเป็น \(100 \times 100\) แทน และลองประมาณหา \(A\) อีกเช่นเดิม จะเห็นว่าสำหรับระบบที่ใหญ่ขึ้นกว่าเดิม ซึ่งมีเซลล์ประสาทเพียงแค่ 100 เซลล์ correlation ของ \(A\) กับ \(A_{approx}\) ลดลงเหลือเพียง 0.57 เท่านั้น

A = create_state_matrix(n_dim=100)
x_vec = simulate_system(A, n_timestep=1000, noise_level=0.5)

n = x_vec.shape[0]
A_approx = np.cov(x_vec[:, :n_timestep - 1], x_vec[:, 1:], rowvar=1)[n:, 0:n]

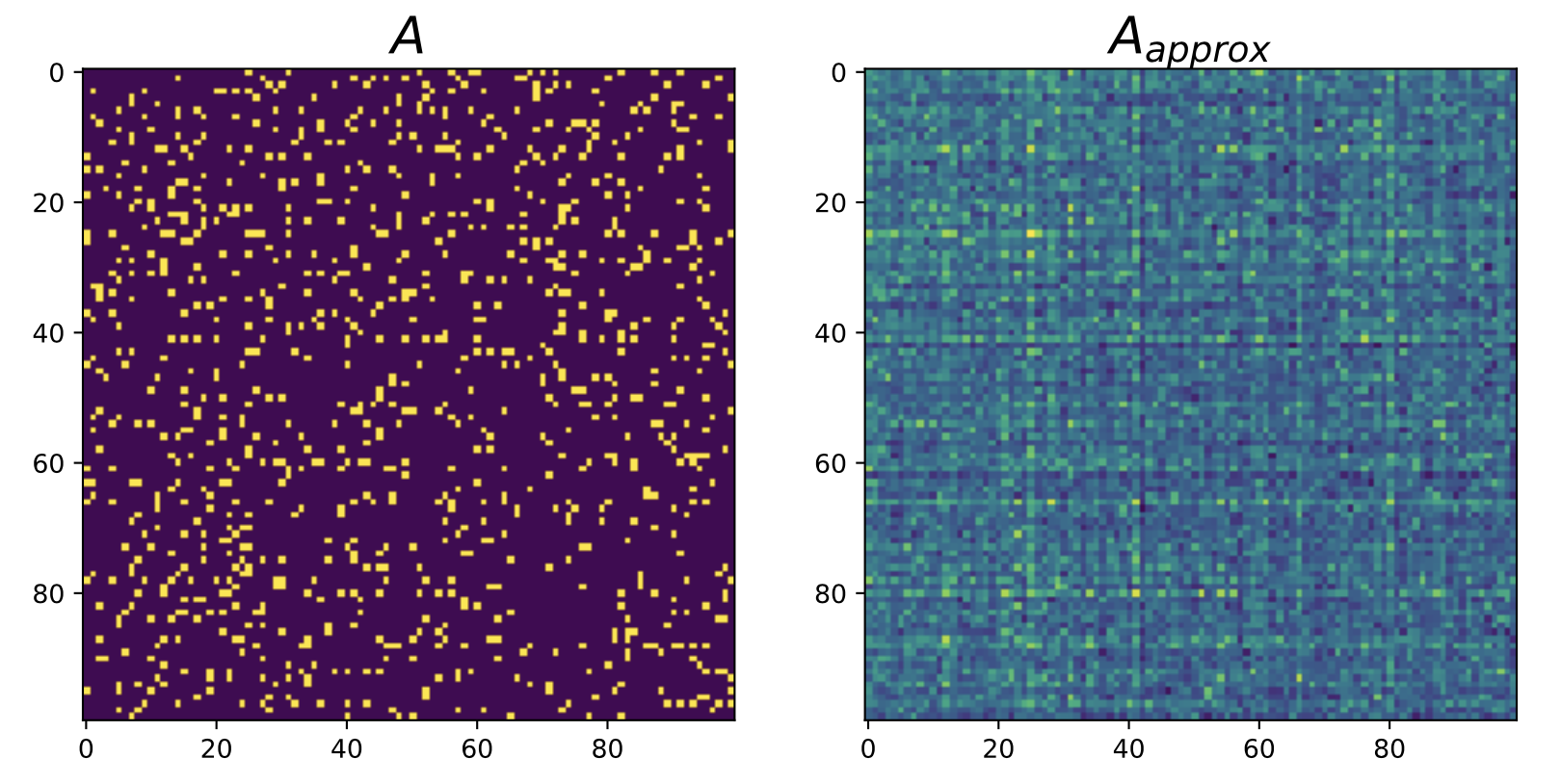
จะเห็นว่าการคำนวณโดยใช้เทคนิคที่ใช้กันมาอย่าง Functional Connectivity ไม่สามารถบอกความสัมพันธ์ของเซลล์ประสาทได้ เมื่อขนาดของระบบใหญ่ขึ้นมากๆเช่นสมองเป็นต้น

ดังนั้นสำหรับการศึกษาสมองนั้น เทคนิคที่คนใช้กันอย่าง Functional Connectivity อาจจะไม่เพียงพอสำหรับการหาความสัมพันธ์ระหว่างเซลล์ประสาทได้ การหาความสัมพันธ์ที่แท้จริงโดยการใช้เทคนิค Causal Inference จึงมีความสำคัญมากๆในการศึกษาสมองนั่นเอง

ถ้าเราสามารถเก็บได้เพียงกลุ่มของเซลล์ประสาท

ลองนึกดูว่าในชีวิตจริงเราไม่สามารถเก็บข้อมูลของเซลล์ประสาททุกเซลล์ได้ แต่ว่าเป็นผลรวมของเซลล์มากกว่าเช่นเวลาเราเก็บข้อมูลจาก fMRI หรือ EEG หรือ ECoG เราวัดผลรวมของเซลล์ประสาททั้งสิ้น การเก็บข้อมูลจากกลุ่มของเซลล์ประสาทยิ่งทำให้เราประมาณ​การเชื่อมต่อของสมองได้ยากขึ้นไปอีกในกรณีนี้

เราลองดูได้จากตัวอย่างด้านล่าง ถ้าเราสามารถเก็บข้อมูลจากเซลล์ประสาทได้เป็นกลุ่มๆ กลุ่มละ 10 เซลล์ เมทริกซ์ที่ใช้รวมการทำงานของสมองนั้นคือเมทริกซ์​ \(B\) นั่นเอง

n, m = A.shape
n_reduce = int(n/10)
B = np.zeros((n_reduce, m))
for i in range(10):
    B[i, i * 10: (i + 1) * 10] = 1
y = B.dot(x_vec) # B here is a observe matrix, e.g. we only observe linear combination of neurons

ด้านบนนั้นเราแค่เพียง map สัญญาณจากเซลล์ประสาท 100 เซลล์ให้เหลือ 10 ด้วยเมทริกซ์ \(B\) ซึ่งสัญญาณที่เราได้ก็คือ \(y\) ซึ่งจะมีขนาด \(10 \times T\) และเราสามารถคำนวณควมสัมพันธ์ระหว่างสัญญาณ y ได้ดังต่อไปนี้

C_y = np.cov(y[:, :n_timestep - 1], y[:, 1:], rowvar=1)
plt.subplot(1, 2, 1)
plt.imshow(A)
plt.subplot(1, 2, 2)
plt.imshow(C_y[n_reduce:, 0:n_reduce])
plt.show()

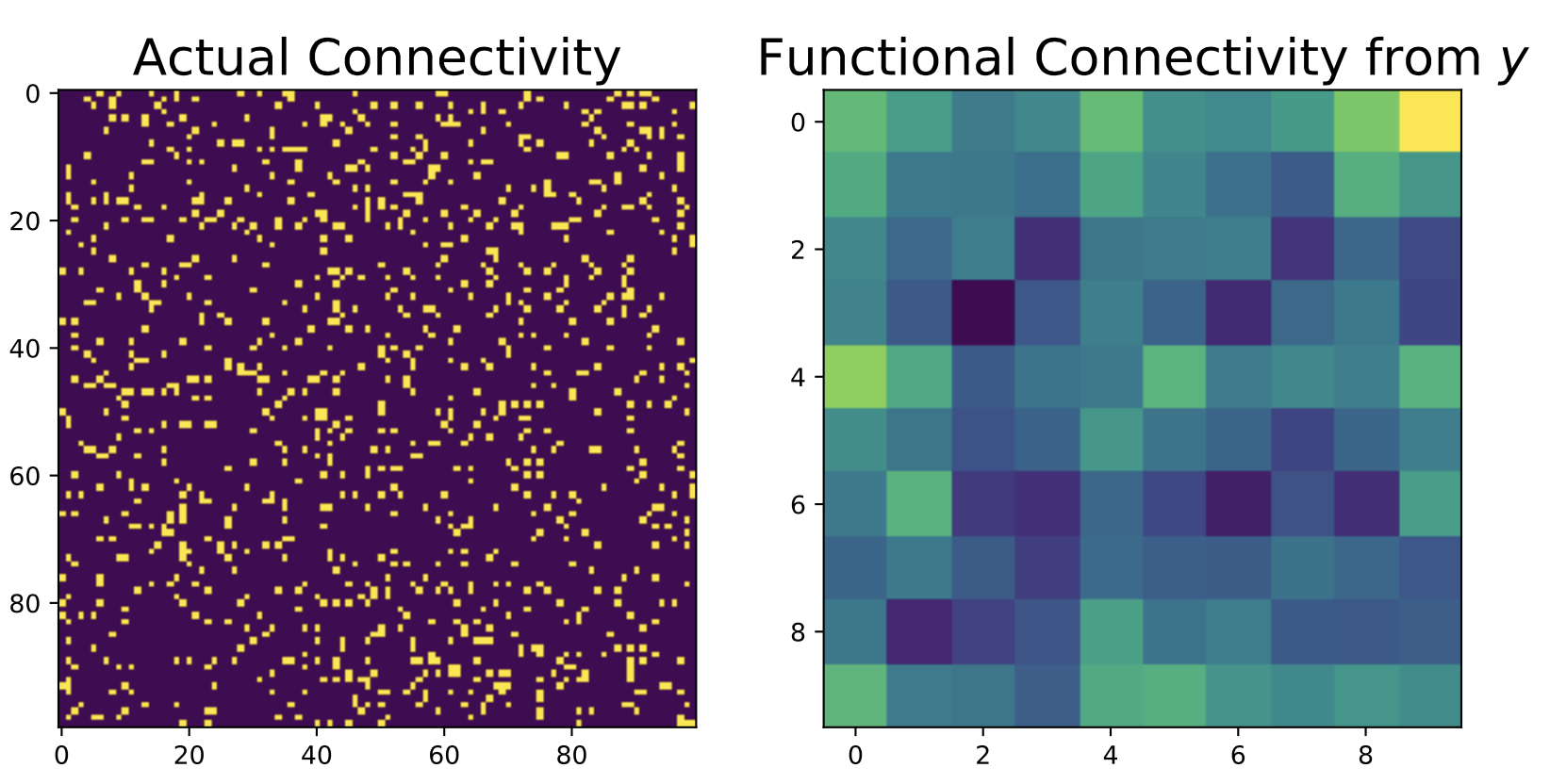
ในกรณีนี้เราประมาณได้เพียงเมทริกซ์ \(C_{y}\) ซึ่งยากที่เราจะบอกได้จริงๆว่าจริงๆแล้วเมทริกซ์ \(A\) หน้าตาเป็นอย่างไรนั่นเอง

ลองนึกถึงในสมองของเรานั้นมีเซลล์ประสาททั้งหมดกว่า 100 ล้านล้านเซลล์ ซึ่งในอุดมคติเมทริกซ์ \(A\) มีขนาดใหญ่มากๆๆๆ การที่เราใช้เทคนิคเพื่อหา Functional Connectivity อาจจะไม่ใช่ทางที่ดีที่สุดสำหรับการศึกษาเซลล์ประสาท ดังนั้นการใช้เทคนิคของการหาความเป็นสาเหตุหรือ Causal Inference จึงสำคัญอย่างยิ่งในการศึกษาประสาทวิทยานั่นเอง

ถึงจุดนี้พูดมากันซะเยอะทีเดียวกว่าจะเข้าใจว่าทำไมเราจำเป็นต้องใช้เทคนิคใหม่ๆมาศึกษาในศาสตร์ของประสาทวิทยา และรวมถึงศาสตร์ต่างๆที่ใกล้เคียงเพราะว่า ในบางครั้งเราไม่สามารถใช้เพียง correlation มาอธิบายปรากฏการณ์ที่เกิดขึ้นได้
ต่อไปเราจะมาดูกันว่าโรงเรียนความคิดของวิชา Causal Inference มีแบบไหนบ้าง โดยจะยังไม่พูดถึงว่าเทคนิคใดดีกว่าแบบใดในโพสต์นี้กัน

3 สำนักของ Causal Inference

ในปัจจุบันมีโรงเรียนความคิดที่สอนด้าน Causal Inference ทั้งหมด 3 รูปแบบหลักๆ

1. Directed Acyclic Graph (DAGs) ซึ่งได้พัฒนามาจากหนังสือ Causality ของ Judea Pearl ที่ออกมาเมื่อปี 2000
2. Causal Discovery ซึ่งพัฒนามาจากกลุ่มนักวิจัยสาขาคอมพิวเตอร์
3. Causal Interence from Economics เป็นศาสตร์ที่พัฒนามาจากกลุ่มนักเศรษฐศาสตร์ โดยมีเทคนิคที่สำคัญๆได้แก่ Randomized Control Trial (RCT), Regression Discontinuity Design (RDD), Instrumental Variable, และอื่นๆ

ส่วนเทคนิคต่างๆที่คนเอามาใช้กันมาจากศาสตร์ใดบ้างและเอามาใช้แตกต่างกันอย่างไร เราจะพูดกันในบล็อกหน้านะ

อารัมภบท

ในบล็อกนี้เราได้จำลองระบบของสมองแบบง่ายและเราเห็นภาพว่าถ้าสมองหรือระบบมีขนาดเล็ก เราสามารถศึกษาระบบได้อยากไม่ยากนัก แต่เมื่อระบบใหญ่ขึ้นมากๆ การประมาณความสัมพันธ์ระหว่างเซลล์สมองทำได้ยากมากๆ (นึกถึงระบบที่มี 100 ล้านล้านเซลล์สมองของคน) นั่นเป็นสาเหตุที่เทคนิคที่ใช้กันในปัจจุบันอย่าง Functional Connectivity ไม่สามารถนำมาใช้ได้อย่างดีนัก การนำความรู้จากศาสตร์อย่าง Causal Inference จึงสามารถนำมาศึกษาการทำงานของระบบใหญ่ๆได้ดีกว่าวิธีคิดแบบเก่าๆ

เรายังไม่ได้พูดถึงว่าจะนำเอา Causal Inference มาใช้งานอย่างไรในบล็อกนี้ แต่ว่าผู้เขียนจะมาเล่าต่ออย่างแน่นอนในบล็อกหน้าๆหลังจากเรียนไปอีกซักพักนึง รอติดตามกันได้เลยฮะ

อ่านเพิ่มเติม

• Could a Neuroscientist Understand a Microprocessor? by Eric Jonas and Konrad Kording
• The Book of Why: The New Science of Cause and Effect by Judea Pearl